이론
PCA는 고차원의 데이터의 분포를 유지한채(최대한 중요한 정보를 유지한채) 차원을 낮추기 위한 알고리즘이다. 고차원에서 저차원으로 변환하는 과정에는 초평면 혹은 벡터에 정사영 혹은 투영(projection) 과정이 수행된다. 우선, 고차원 데이터에 대한 데이터의 분포를 파악하는 것이 중요하다. 분포는 데이터가 어느정도 넓게 퍼져있는가를 의미한다.

만약 위와 같은 2차원 파란색 데이터가 존재한다고 가정할 때, 1~3번 선중 어느 선이 가장 데이터를 잘 표현한다고 할 수 있을까? 직관적으로 보았을 때, 데이터가 가장 넓게 분포한 방향으로 기울어진 2번 선을 선택할 수 있을 것이다.

2번 선(벡터)에 대해 사영시키면 빨간점으로 이루어진 데이터들을 볼 수 있다. 이 점들은 하나의 선(1차원)으로 표현되며 기존에 2차원 파란색 데이터의 분포를 잘 유지하고 있으므로 차원 축소(dimensionality reduction)의 효과가 있다.
...
먼저 이 선을 찾기 위해서는 우리는 공분산 행렬(covariance matrix)이 필요하다. 먼저 공분산 행렬을 구하는 과정을 살펴보자.
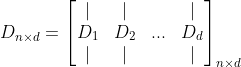
행렬 $D$는 $n$개의 데이터 샘플을 위와 같이 표현할 수 있다. 각 샘플은 $d$개의 feature 혹은 차원을 가지고 있다. 즉, 행은 데이터 샘플의 갯수, 열은 각 데이터 샘플의 feature(차원)수를 의미한다.

$mean(D, axis=0)$는 행렬 $D$에 대해 0 번째 차원에 대한 평균을 구하라는 의미이다. 행렬 $D$는 $n \times d$의 차원을 가지고 있으며, 0 번째 차원은 즉, $n$을 의미한다. 즉, $n$개의 모든 샘플에 대해 각 feature별 평균을 구하라는 의미이다. (만약 axis가 1이라면 $d$에 대해 각 샘플별 평균을 구하게 되므로 각 샘플마다 모든 특징값의 평균을 구하라는 의미가 된다.) 고로, 행렬 $X$의 열벡터($X_1 ~ X_d$)는 각 feature별 편차(분산)를 의미한다.

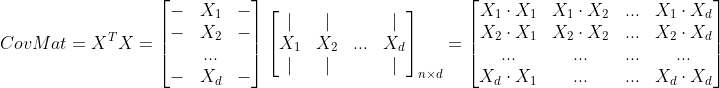
마지막으로 공분산 행렬을 구하는 과정이다. 행렬 $X$에 자신의 전치행렬을 곱하여 대칭을 이루는 정방행렬이 나온다. 공분산 행렬의 각 원소는 행렬곱 과정에서 자연스럽게 feature별 편차 벡터($X_1 ~ X_d$)를 내적하므로 feature별 분포의 유사도(두 벡터의 내적은 유사도를 의미하므로)로 해석할 수 있다.
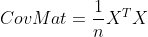
하지만, 위 식 그대로 공분산 행렬을 구현할 경우 행렬의 원소가 데이터 샘플이 많아질수록 방대하게 커지기 때문에 데이터 샘플의 갯수 $n$만큼 나눠주어야 한다.
...
이제 데이터의 주성분 축을 찾기 위해서는 공분산 행렬을 고유값 분해를 진행하면 된다. 고유값과 고유벡터를 구하는 과정은 해당 포스트를 참고한다. 공분산 행렬의 고유 벡터 $v_n$는 데이터의 주성분 축이 되고, 고유값 $\lambda_n$은 해당 주성분 축으로의 분포를 의미한다.

...
대칭 행렬의 경우 고유벡터가 서로 직교하는 성질이 있다.
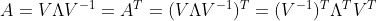
$\Lambda$는 대칭 행렬이므로 $\Lambda = \Lambda^T$이고, $(V^{-1})^T = (V^{T})^{-1}$ 이므로,
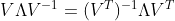
행렬 $V$는 직교하는 고유벡터들의 집합이므로 직교 행렬이다. 직교행렬은 $V^{-1} = V^T$ 인 성질이 있으므로,
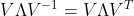
즉, $A = V \Lambda V^{-1} = V \Lambda V^T$ 이 성립한다.
참고
https://angeloyeo.github.io/2019/07/27/PCA.html
주성분 분석(PCA) - 공돌이의 수학정리노트
angeloyeo.github.io
PCA(주성분 분석) 정리
목차 사전 지식 PCA 의미 계산 방법 정리 PCA 단점 사전 지식 공분산 - x와 y의 공분산은 모든 데이터에 대해 (x데이터 - x의 평균) * (y데이터 - y의 평균)의 평균을 뜻한다. - 각 확률 변수(X, Y)의 평균
dhpark1212.tistory.com
'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| SVD (Singular Value Decomposition) (0) | 2022.01.17 |
|---|---|
| 고유값 분해 (Eigen-value Decomposition) - 2 (1) | 2021.11.23 |
| 고유값 분해 (Eigen-value Decomposition) - 1 (0) | 2021.11.23 |
| QR 분해 (QR Decomposition) - 2 (0) | 2021.10.05 |
| QR 분해 (QR Decomposition) - 1 (0) | 2021.10.05 |