# 9. 고유값 분해 (Eigen-value Decomposition) - 1

고유값 분해를 다루기 이전에 고유값과 고유벡터의 개념에 대해서 먼저 다루려고 한다. 먼저 이 포스트를 보기 이전에 선형변환에 대한 개념을 숙지하고 보는 것을 추천한다. 

 

우리는 선형변환을 하나의 함수로써 생각했다. 예를 들어 임의의 벡터 x를 행렬 A의 선형변환 연산을 취했을 경우, 또 다른 벡터가 나오는 것처럼..

 

선형변환

 

보통은 선형변환을 통해 크기와 방향 모두 바뀐다. 하지만, 우리가 이번에 다룰 선형변환은 크기만 바뀌는 경우에 대해서만이다.

 

그렇다면, 고유값과 고유벡터는 어떤 의미를 지닐까? 고유값은 방향이 변하지 않은 벡터에 대해 어느정도 크기가 바뀌었는가의 의미이고, 고유벡터는 해당 고유값에 대응하는 벡터 x를 의미한다. 수학적으로는 다음과 같이 정의할 수 있다.

 

 

위 식을 이항하면 다음과 같이 표현할 수 있다.

 

 

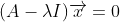
여기서 I는 identity matrix를 의미한다. 그리고 위 식이 만족하기 위해서는 벡터 x가 0이 되는 경우(trivial solution)를 피해야 한다. 그렇지 않을 경우 모든 고유값에 대해 위 식이 성립하는 오류가 발생한다.

 

우리가 trivial solution을 피하기 위해서는 다음과 같은 조건을 만족해야 한다. trivial solution에 대해 간단히 설명하자면, Ax = 0 의 식이 존재할 때, 행렬 A가 가역행렬일 경우 벡터 x는 0임을 의미한다. 고로, 행렬 A를 가역행렬이 아니기 위해서는 행렬식이 0이어야 trivial solution을 피할 수 있는 것이다.

 

 

 

위와 같은 행렬 A가 존재한다고 가정하자. 우리는 이 행렬 A에 대해 고유값과 고유 벡터를 구할 것이다.

 

 

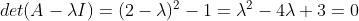
우리는 행렬식을 통해 행렬 A의 고유값을 구했다. 그럼 이제 각각의 고유값에 해당하는 고유벡터를 구할 차례이다. 맨 처음에 작성했던 식에 각각의 고유값을 대입하여 연립방정식의 해를 구하면 고유벡터를 도출할 수 있다.

 

 

 

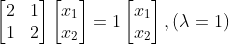
참고

위 내용은 다음 링크에서 공부한 내용을 정리한 것입니다.

https://angeloyeo.github.io/2019/07/17/eigen_vector.html

고윳값과 고유벡터 - 공돌이의 수학정리노트

https://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=61635595&qb=bm9udHJpdmlhbA==&enc=utf8&section=kin&rank=5&sort=0&spq=0&pid=fIub5z331xhssZAISPRssv--275758&sid=S59ddmxJn0sAAEVsLqY 

선형대수학문제 입니다.