사전 지식
직교행렬 (othogonal matrix)
직교행렬은 각 열벡터가 서로 직교하는 행렬을 의미하며, 각 열벡터의 스칼라값이 1일 경우, 해당 행렬은 정규직교행렬이라고 한다.

대각행렬 (diagonal matrix)
대각행렬은 주대각선 요소에만 값이 존재하는 행렬을 의미한다. 그러므로 대각행렬에 대한 전치행렬(transpose matrix)은 결국 자기 자신이다.

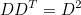
고유값 분해 (eigen value decomposition)
SVD (Singular Value Decomposition)
SVD의 정의는 특정 벡터들이 서로 직교할 때, 해당 벡터들에 선형변환 $A_{m \times n}$를 취한 경우, 선형변환된 벡터들이 크기는 변하더라도 여전히 직교하는가? 의 의미를 지니고 있다.

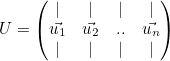
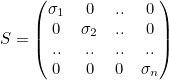
행렬 $V_{m \times m}$는 선형변환 이전의 직교하는 벡터들의 집합이다. 행렬 $U_{n \times n}$는 선형변환 이후의 직교하는 벡터들의 집합이다. 행렬 $S_{m \times n}$는 scaling factor를 주대각선의 요소로 갖고있는 행렬이다.


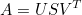
즉, 선형변환 행렬 $A$는 위 식과 같이 전개할 수 있으며, m 차원 공간의 벡터들을 n 차원 공간의 벡터들로 투영함과 동시에 아까 크기가 변할 수 있다고 했는데, 그 크기는 행렬 $S$의 scaling factor에 의해 결정된다.

그림으로 이해해보자. 3차원 공간의 벡터 $v_1, v_2, v_3$가 있다고 가정할 때, 이 벡터들에 $xy$평면에 projection하는 선형변환 $A$를 취했다. 이 경우, 각 벡터들의 z값은 더 이상 반영하지 않기 때문에, 벡터 $v_3$의 scaling factor는 0이 되어 더 이상 2차원 공간에 투영되지 않는다. (이해를 쉽게 하기 위하여 선형 변환 이후에도 z축을 남겨둔 것이다.)
SVD 계산법

선형변환 $A$는 SVD의 정의에 따라 다음과 같이 분류할 수 있음을 확인했다. 그에 대한 전치행렬은 다음과 같이 전개할 수 있다.



선형변환 $A$의 앞뒤에 선형변환의 전치행렬을 곱하면 다음과 같이 전개할 수 있다. 행렬 $AA^T$와 $A^TA$를 고유값 분해를 진행하면 각각의 형태가 나오는 것을 확인할 수 있다. 즉, 행렬 $AA^T$를 고유값 분해하여 얻은 고유벡터를 정규화하면 정규직교행렬 $U$를 얻을 수 있다. 반대로 행렬 $A^TA$를 고유값 분해하여 얻은 고유벡터를 정규화하면 정규직교행렬 $V$를 얻을 수 있다. 그리고 고유값 분해를 하는 과정에서 얻은 scaling factor는 행렬 $S^2$이므로 이를 square root를 취해주면 행렬 S도 도출해낼 수 있다.
SVD의 활용

선형변환 $A$는 최종적으로 위와 같은 형태로 표현할 수 있다. 즉, scaling factor에 따른 layer($\vec{u_k}\vec{v_k}$)로 분류했다고 해석할 수 있다. 이러한 해석을 통해 이미지 압축에도 활용될 수 있다. SVD를 진행하여 각 layer별로 scaling factor가 높은순으로 정렬한 다음, scaling factor가 낮은 layer들을 반영하지 않으면, 주된 특성들을 고려한 채로 이미지의 용량을 줄일 수 있는 것이다.
참고
https://angeloyeo.github.io/2019/08/01/SVD.html
특이값 분해(SVD) - 공돌이의 수학정리노트
angeloyeo.github.io
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=tlaja&logNo=220726154312
선형대수학 < 특이값 분해 SVD(Singular Value Decomposition) >
1. SVD(Singular Value Decomposition) : 특이값 분해라고 부르며 (1)식과 같이 행렬A 를 특정 구조...
blog.naver.com
'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| PCA (Principal Component Analysis) (0) | 2022.03.07 |
|---|---|
| 고유값 분해 (Eigen-value Decomposition) - 2 (1) | 2021.11.23 |
| 고유값 분해 (Eigen-value Decomposition) - 1 (0) | 2021.11.23 |
| QR 분해 (QR Decomposition) - 2 (0) | 2021.10.05 |
| QR 분해 (QR Decomposition) - 1 (0) | 2021.10.05 |