저번 포스트에서는 고유값과 고유벡터에 대해서 알아보았다. 이번 포스트에서는 실제로 행렬 A에 대해 고유값 분해를 하는 과정에 대해 알아보겠다.
우선, $n \times n$ 행렬 A에 대해 고유값과 그에 대응하는 고유벡터들을 구해야한다.
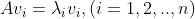
그리고 고유벡터들($v_i$)을 모아둔 행렬 $V$를 다음과 같이 정의할 수 있다.
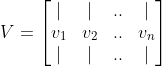
두 번째 식에 각각의 열벡터(고유벡터)에 해당하는 고유값을 곱해보자.
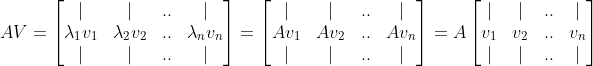
그 결과 행렬 A와 V로 위와 같이 표현할 수 있다. 마지막으로 고유값들을 대각성분에 모아둔 행렬을 보자.

네 번째 식을 통해 AV 행렬을 인수분해가 가능하다.

다섯번째 식에서 각 열벡터(행렬 V의 고유벡터)들이 선형독립이라면 아래와 같이 행렬 A를 표현할 수 있다.
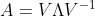
사실 아직 행렬 A를 분해하는 의미를 설명하지 않았다. 이는 기하학적으로 표현할 수 있다. 6번째 식에서 보다시피 현재 행렬 A를 V와 \Lambda, V의 역행렬로 분해했다.
- 행렬 V는 고유벡터들의 집합을 의미하며, 고유벡터들은 크기가 1인 벡터로 방향성만 지니고 있다. 고로, 회전과 비슷한 변환을 보여준다.
- 행렬 \Lambda는 네 번째 식에서 볼 수 있듯이 대각성분에만 값이 존재하여 상하좌우로만 스케일링해주는 효과가 있다.
- 마지막으로 V의 역행렬은 행렬 V의 변환의 반대로 동작하기 때문에 다시 회전한만큼 반대로 회전한다.
결론
행렬 A에 대한 선형변환을 기하학적인 의미로 세 가지 동작으로 분류했다. '회전', '스케일링', '역회전'으로 표현한 것이다.
참고
위 내용은 다음 링크에서 공부한 내용을 정리한 것입니다.
https://angeloyeo.github.io/2020/11/19/eigen_decomposition.html
고윳값 분해(eigen-value decomposition) - 공돌이의 수학정리노트
angeloyeo.github.io
https://rfriend.tistory.com/163
[선형대수] 선형독립(linearly independent), 선형종속(linearly dependent)
이번 포스팅에서는 선형독립 혹은 1차 독립(linearly independent)과 선형종속 혹은 1차 종속(linearly dependent)에 대해서 알아보겠습니다. 선형독립 혹은 1차 독립 (linearly independent) 개념은 나중에 이어..
rfriend.tistory.com
'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| PCA (Principal Component Analysis) (0) | 2022.03.07 |
|---|---|
| SVD (Singular Value Decomposition) (0) | 2022.01.17 |
| 고유값 분해 (Eigen-value Decomposition) - 1 (0) | 2021.11.23 |
| QR 분해 (QR Decomposition) - 2 (0) | 2021.10.05 |
| QR 분해 (QR Decomposition) - 1 (0) | 2021.10.05 |