이론

함수는 정의역(Domain)과 공역(Codomain)간의 1대 1 mapping 관계를 의미한다. 함수는 크게 선형함수와 비선형함수로 분류할 수 있다. 선형함수는 말그대로 기하학적으로 Linear한 형태의 함수를 의미한다. 선형함수에 해당하기 위한 조건은 다음과 같이 2가지가 있다.

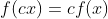
이제 함수에 대해 간단하게 짚었으니, 변환(transformation)에 대해 알아볼 차례이다. 변환은 입출력이 벡터인 함수를 의미한다. 특히, 입력 벡터와 출력 벡터의 차원이 동일한 경우 ($n$-벡터와 $m$-벡터에 대해 $n=m$인 경우) 변환이라 칭하지 않고 연산자(operator)라고 한다.

선형시스템에서 행렬 A는 ($m \times n$ 행렬) $n$-벡터를 입력으로 받아 $m$-벡터를 출력으로 하는 변환($T$)으로 볼 수 있다. 이 변환은 행렬 A가 정의하기 때문에 행렬 변환 (matrix transformation)이라고 한다.

동시에 행렬 변환은 선형 함수의 성질 또한 만족하기 때문에 선형 변환 (linear transformation) 이다.


이제 선형 변환을 구현하는 방법에 대해 알아보겠다. 크게 3단계로 나눌 수 있다.
1. 구현하고자 하는 기능의 입출력이 벡터로 정의되는지 확인한다.
2. 구현하고자 하는 기능이 선형 함수의 조건을 만족하는지 확인한다.
3. 입력이 $n$-벡터이고 출력이 $m$-벡터이면 $m \times n$ 표준행렬을 구성한다.
3-1. $n$-차원 표준기저벡터 {e1, e2, .. , en}을 생각한다.
3-2. 각 $n$-차원 표준기저벡터 $e_i$에 대해, 우리가 원하는 기능을 동작시켜 얻을 결과인 $m$-차원 벡터 $T(e_i)$를 표준행렬의 각 열에 적는다.
직접 문제를 통해 무슨 의미인지 확인해보자.
1번 문제) 2차원 벡터를 입력받아 x축에 projection(투영)하는 linear transform을 구현.
1. 구현하고자 하는 기능의 입출력이 벡터로 정의되는지 확인한다.
입력 : 2차원 벡터, 출력 : 2차원 벡터
2. 구현하고자 하는 기능이 선형 함수의 조건을 만족하는지 확인한다.
- 두 벡터 $v_1$, $v_2$가 존재한다고 가정할 때, $x$축에 투영한 벡터들의 $x$좌표값을 더한 결과와 $v_3$벡터($v_1+v2$)를 $x$축에 투영한 $x$좌표값의 결과와 동일
- 벡터 $v_1$과 벡터 $t_1$($v_1$의 $x$축 투영 벡터)이 존재한다고 가정했을 때, $v_1$에 스칼라 $c$를 먼저 곱하고 투영한 $x$축 좌표값과 $t_1$의 $x$좌표값에 $c$를 곱한 값은 동일
3. 입력이 $n$-벡터이고 출력이 $m$-벡터이면 $m \times n$ 표준행렬을 구성한다.
3-1. $n$-차원 표준기저벡터 {$e_1$, $e_2$, .. , $e_n$}을 생각한다.
$n$은 2이므로, 2-차원 표준기저벡터 {$e_1$, $e_2$}를 생각한다.
3-2. 각 $n$-차원 표준기저벡터 $e_i$에 대해, 우리가 원하는 기능을 동작시켜 얻을 결과인 $m$-차원 벡터 $T(e_i)$를 표준행렬의 각 열에 적는다.
$e_1$ = [1, 0], $e_2$ = [0, 1] 벡터이다. 우리가 원하는 것은 $x$축에 투영되는 것이기 때문에 각 기저 벡터를 $x$축에 투영시키면 $T(e_1)$ = [1, 0], $T(e+2)$ = [0, 0]이 되어 $m \times n$ 표준행렬 $A$의 각 열에다가 stack하면 다음과 같이 구할 수 있다.



2번 문제) 2차원 벡터를 입력받아 해당 벡터를 반시계 방향으로 $\theta$만큼 회전하는 linear transform 구현.
1. 구현하고자 하는 기능의 입출력이 벡터로 정의되는지 확인한다.
입력 : 2차원 벡터, 출력 : 2차원 벡터
2. 구현하고자 하는 기능이 선형 함수의 조건을 만족하는지 확인한다.
- 두 벡터 $v_1$, $v_2$가 존재한다고 가정할 때, 두 벡터를 합하고 회전시킨 벡터와 각각 회전시키고 합한 벡터와 동일
- 벡터 $v_1$가 존재한다고 가정했을 때, $v_1$을 회전시키고 스칼라 $c$배를한 벡터와 스칼라 $c$배를 먼저하고 회전시킨 벡터와 동일
3. 입력이 $n$-벡터이고 출력이 $m$-벡터이면 $m \times n$ 표준행렬을 구성한다.
3-1. $n$-차원 표준기저벡터 {$e_1$, $e_2$, .. , $e_n$}을 생각한다.
$n$은 2이므로, 2-차원 표준기저벡터 {$e_1$, $e_2$}를 생각한다.
3-2. 각 $n$-차원 표준기저벡터 $e_i$에 대해, 우리가 원하는 기능을 동작시켜 얻을 결과인 $m$-차원 벡터 $T(e_i)$를 표준행렬의 각 열에 적는다.

위 그림의 좌측에 $e_1$을 반시계 방향으로 회전시키면 [cos(-$\theta$), sin(-$\theta$)]
위 그림의 우측에 $e_2$을 반시계 방향으로 회전시키면 [cos(90-$\theta$), sin(90-$\theta$)] = [sin($\theta$), cos($\theta$)]

'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| QR 분해 (QR Decomposition) - 2 (0) | 2021.10.05 |
|---|---|
| QR 분해 (QR Decomposition) - 1 (0) | 2021.10.05 |
| 좌표계 변환 (Change of Basis) (0) | 2021.09.23 |
| 열 공간 (Column Space) (0) | 2021.06.20 |
| 선형 조합 (Linear Combination) (0) | 2021.06.18 |