Sequence Data (시퀀스 데이터)
이번 포스트에서는 순환 신경망(Recurrent Nerual Network, RNN)에 대해 다룬다. RNN은 입출력을 시퀀스(=시간) 단위로 처리하는 모델이다. 고로, 시계열 데이터를 처리하는데에 적합하다. RNN을 다루기 이전에 시퀀스에 대해 간략하게 짚고 넘어가자.
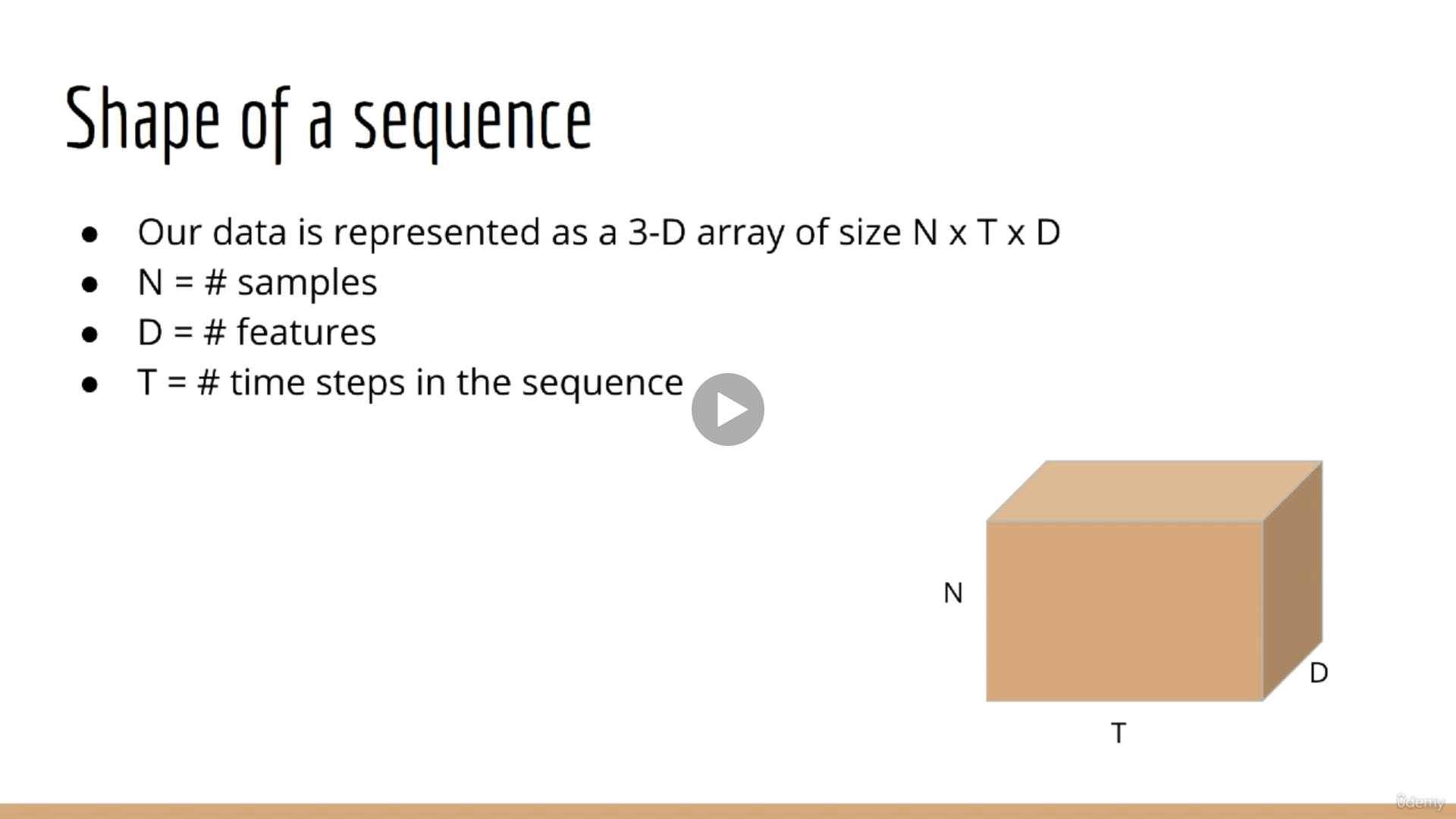
이전에 다루던 데이터는 시간을 고려하지 않은 데이터들이었다. Tabular 데이터는 $N \times D$의 모양을 가지고 있다. 이때, $N$은 데이터 샘플의 수, $D$는 피처의 수다. 여기에 시간을 고려한 데이터를 하나의 배열에 표현하려면 $N \times T \times D$로 표현할 수 있다. 그리고 RNN의 각 시퀀스의 입력에 대입되는 모양은 $N \times 1 \times D$가 될 것이다.


예를 들어 자동차의 GPS로 기록한 이동 경로를 모델링 하고 싶다고 가정해보자. 이때 $N$은 한 사람의 이동 경로가 될 것이다. $D$는 위도와 경도를 포함하므로 2일 것이다. $T$는 30분 동안 매초마다 기록했다고 가정하면 1800이다.
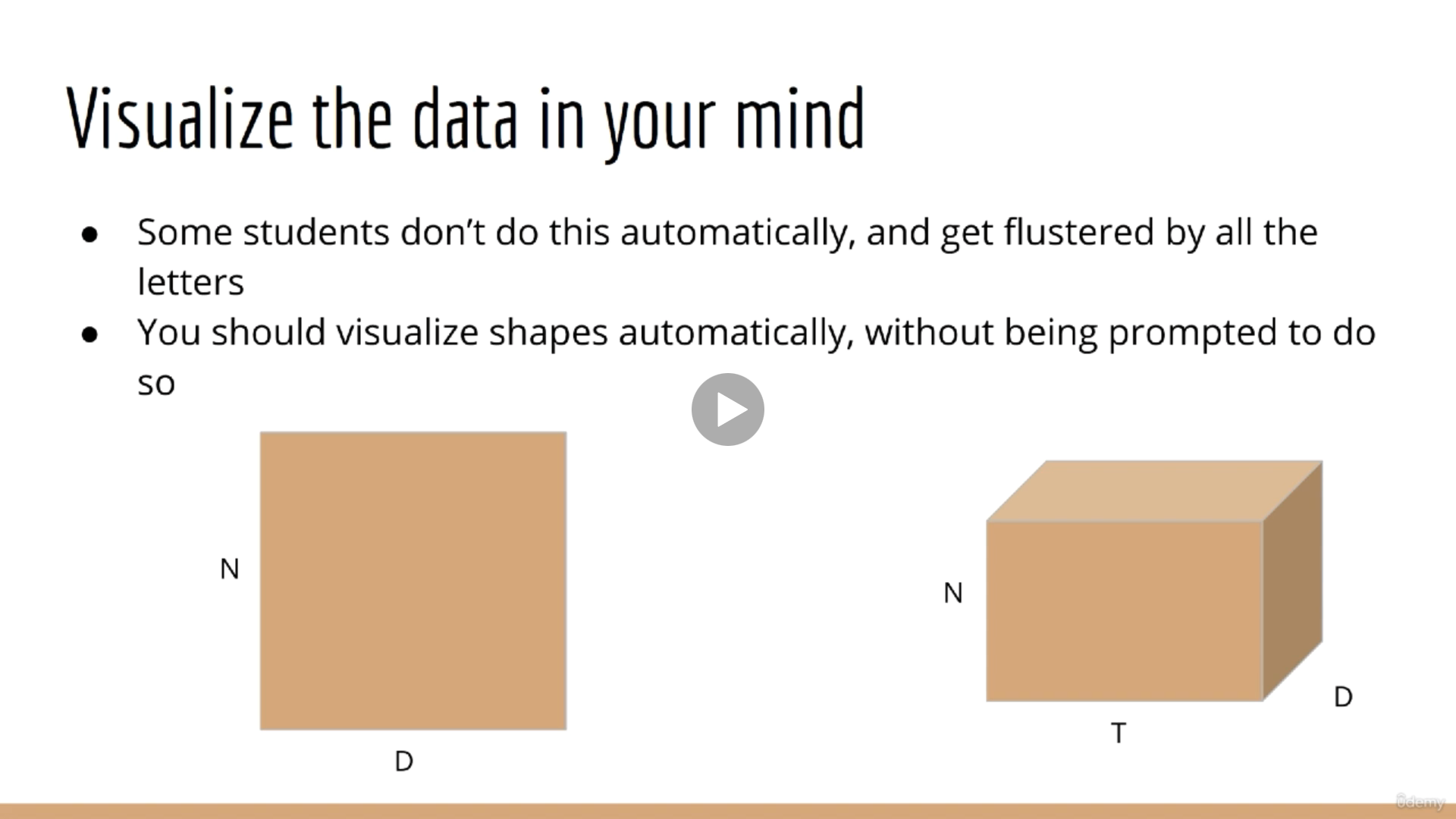
시퀀스 데이터를 생각할 때 위의 이미지처럼 생각하면 도움이 된다. $N \times D$ (샘플 수 $\times$ 피처 수) 행렬의 시간별 데이터의 집합이다.

위 이미지처럼 가변 길이의 시퀀스가 존재하는 경우가 있다. (샘플들의 시퀀스가 일치하지 않는 경우) 예시로 문장을 들 수 있다. 문장들의 길이가 전부 다르기 때문이다. 텐서플로우에서 pad_sequence와 같은 메소드를 통해 시퀀스의 길이를 통일할 수 있다.
RNN (Recurrent Neural Network)
필자가 알기로는 "RNN - LSTM - Encoder, Decoder - Transformer(based on attention)" 대충 이런 순서로 발전해온 것으로 안다. 아무튼.. 최신 기술의 근원인 RNN부터 기본을 다지려고 한다.

앞서 배운 CNN은 출력층의 한 방향으로만 값이 향했다. 이러한 신경망을 피드 포워드 신경망(Feed Forward Neural Network)라고 한다. 반면에 RNN은 피드 포워드 신경망에 속하지 않는다. 왜냐하면, 출력으로 향하는 방향과 동시에 다음 시퀀스로 향하는 방향 두 가지가 존재하기 때문이다. $x$는 입력 벡터, $y$는 출력 벡터를 의미한다. $t$는 각 시퀀스를 의미하며, 좌항에 있는 다이어그램을 시퀀스 단위로 펼쳐서 표현하면 우항에 있는 다이어그램처럼 표현할 수 있다.
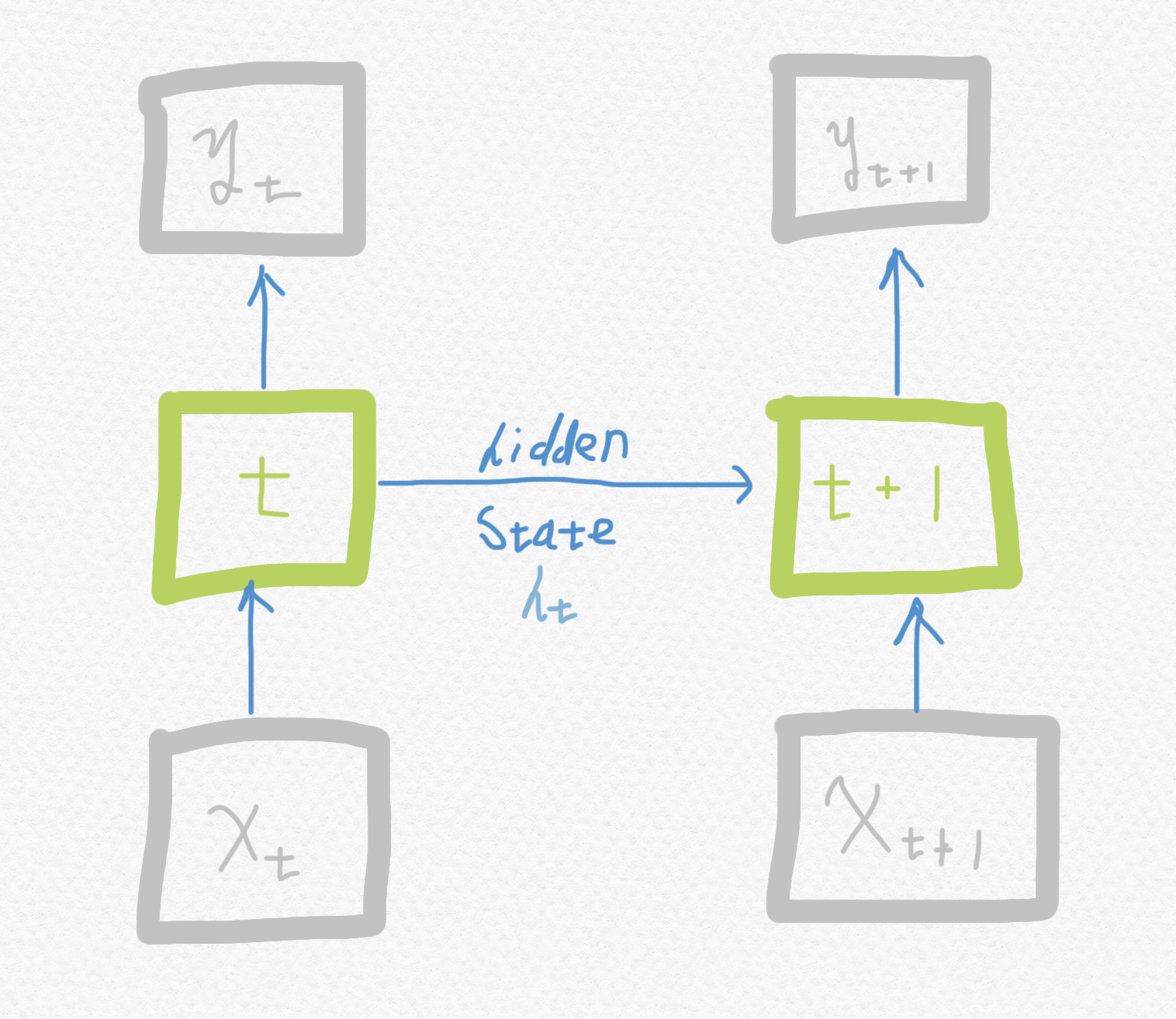
초록색 노드는 셀(cell) 이라고 표현한다. 셀의 역할은 각 시퀀스의 내용을 기억하기 때문에 메모리 셀이라고도 표현한다. 셀이 저장하는 내용은 은닉 상태(hidden state)라고 표현한다. $t+1$ 셀은 $t$ 셀이 저장하고 있는 내용($h_{t}$)과 $t+1$ 시퀀스의 데이터($x_{t+1}$)를 입력받는다.
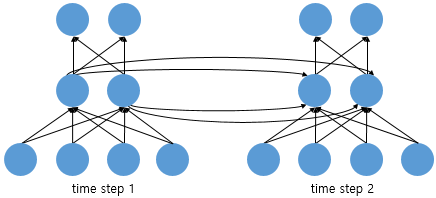
위 그림은 뉴런 단위로 시각화한 RNN의 모습이다. 가운데에 있는 뉴런 2개가 은닉층의 뉴런으로 다음 시퀀스의 은닉층에 값을 전달하는 것을 확인할 수 있다.

RNN은 입력과 출력의 벡터의 차원에 따라 다양한 작업을 수행할 수 있다. 예를 들어 일 대 다(one-to-many)는 사진을 설명할 수 있다. 다 대 일(many-to-one)같은 경우 스팸 메일 분류 문제를 해결할 수 있고, 다 대 다(many-to-many)같은 경우 개체명 인식이나 품사 태깅같은 작업이 가능하다.

RNN 모델을 수식화하면 다음과 같다.
$h_{t} = tanh(W_{x}x_{t} + W_{h}h_{t-1} + b)$
$y_{t} = f(W_{y}h_{t} + b)$ (단, $f$는 비선형 활성화 함수 중 하나)
RNN의 은닉층 연산은 이전 시퀀스의 메모리 셀에 저장된 값(은닉 상태)를 반영하여 현재 시퀀스의 은닉 상태를 도출하는 과정이다. 은닉층 연산은 벡터와 행렬 연산으로 이해할 수 있다. (하나의 시퀀스에서) 입력 벡터 $x_{t}$의 차원을 $d$라고 하고, 은닉 상태의 크기를 $D_{h}$라고 할때, 각 벡터와 행렬의 크기는 다음과 같다.
$W_{x} : (D_{h} \times d)$
$x_{t} : (d \times 1)$
$W_{h} : (D_{h} \times D_{h})$
$h_{t-1} : (D_{h} \times 1)$
$b : (D_{h} \times 1)$
배치의 크기가 1이고, $d$와 $D_{h}$를 4로 가정했을 때, RNN의 은닉층 연산을 그림으로 표현하면 다음과 같다.


실제로 RNN에 입력되는 텐서의 크기는 다음과 같다. 위에서 입력 벡터의 차원인 $d$는 input_dim에 해당하고, 하나의 은닉층에 대한 연산이었기 때문에 1이었지만 실제로는 input_length의 하나의 시퀀스이다.
'[AI] - Neural Network' 카테고리의 다른 글
| Long Short-Term Memory (LSTM) - Theory (0) | 2021.12.09 |
|---|---|
| Recurrent Neural Network (RNN) - Code (0) | 2021.12.07 |
| Convolution Neural Network (CNN) - Code (0) | 2021.05.06 |
| Convolution Neural Network (CNN) - Theory (0) | 2021.05.03 |
| ILSVRC 2012 Dataset (0) | 2021.04.29 |