지난 포스트에서는 순환 신경망 (RNN)에 대해 다루었다. RNN은 시퀀스 데이터를 처리하기에 적합하지만, Gradient vanishing 현상이 존재한다. Gradient vanishing은 신경망에서 은닉층을 거칠수록 (역전파를 통해 가중치를 편미분한) 기울기가 소실되어 학습이 느려지는 현상을 말한다. RNN에서 Gradient vanishing을 직관적으로 설명하면 문장이 길어질수록 앞의 내용을 잊어버리고 뒤에서 엉뚱한 추론을 한다는 의미이다. (역전파와 Gradient vanishing에 관련된 내용은 추후에 포스트에서 자세하게 다루겠다.)
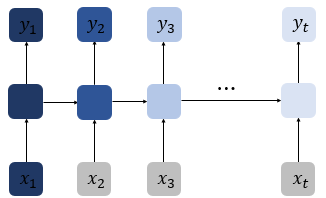
RNN의 Gradient vanishing 문제를 보완하기 위해 메모리 셀에 단순히 은닉 상태(hidden state)뿐만이 아닌 셀 상태(cell state)의 개념을 도입하여 장기 기억에 효과를 보이는 모델이 Long Short-Term Memory이다.

위 그림은 LSTM의 메모리 셀이다. LSTM의 메모리 셀에는 망각 게이트(forget gate), 입력 게이트(input gate), 출력 게이트(output gate) 세 가지의 게이트가 존재한다. 위 그림에서 문자들의 의미를 살펴보자.
- σ는 시그모이드 함수를 의미한다.
- tanh은 하이퍼볼릭탄젠트를 의미한다.
- $C_{t}$는 t 시퀀스(시점)의 셀 상태를 의미한다.
- $W_{xi}, W_{xg}, W_{xf}, W_{xo}$는 $x_{t}$와 함께 각 게이트에서 사용되는 4개의 가중치이다.
- $W_{hi}, W_{hg}, W_{hf}, W_{ho}$는 $h_{t-1}$와 함께 각 게이트에서 사용되는 4개의 가중치이다.
- $b_i, b_g, b_f, b_o$는 각 게이트에서 사용되는 4개의 편향이다.
망각 게이트 (forget gate)

$f_t = \sigma(W_{xf}x_{t} + W_{hf}h_{t-1} + b_f)$
망각 게이트는 기억을 삭제하기 위한 게이트이다. 시그모이드 함수를 거치면 0과 1사이의 값이 나오게 되는데, 0에 가까울수록 기억이 많이 삭제된 것이다.
입력 게이트 (input gate)
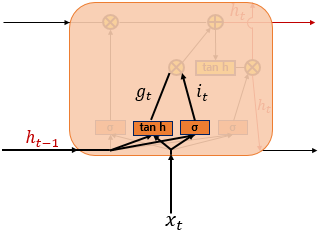
$i_t = \sigma(W_{xi}x_{t} + W_{hi}h_{t-1} + b_i)$
$g_t = tanh(W_{xg}x_t + W_{hg}h_{t-1} + b_g)$
입력 게이트는 현재 정보를 기억하기 위한 게이트이다. $i_t$는 시그모이드 함수를 거치기 때문에 0과 1사이의 값이 나온다. $g_t$는 하이퍼볼릭탄젠트를 거쳐서 -1과 1사이의 값이 나온다.
셀 상태 (cell state, 장기 상태)

$C_t = f_t \circ C_{t-1} + i_t \circ g_t$
$\circ$은 원소별 곱(entrywise product)를 의미한다. 즉, 두 행렬의 같은 위치의 성분끼리 곱하는 것을 의미한다.
삭제 게이트와 입력 게이트의 의미를 살표보자. 삭제 게이트의 값인 $f_t$가 0이라면 이전 셀 상태 $C_{t-1}$를 반영하지 않는다는 의미가 된다. 반면 1일 경우 $C_{t-1}$가 온전히 반영된다. 즉, 삭제 게이트의 의미는 이전 셀 상태를 어느정도 반영하는지를 의미한다. 입력 게이트의 $i_t$가 0일 경우 $g_t$를 전혀 반영하지 않고 이전 셀 상태에만 의존한다. 반면 1인 경우 온전히 $g_t$를 반영한다.
출력 게이트와 은닉 상태 (단기 상태)

$o_t = \sigma(W_{xo}x_t + W_{ho}h_{t-1} + b_o)$
$h_t = o_t \circ tanh(C_t)$
출력 게이트는 현재 시퀀스의 $x$값과 이전 시퀀스의 은닉 상태 $h_{t-1}$가 시그모이드를 거친 값이며, 이를 현재 셀 상태와 원소별 곱을 거친다. 다음 메모리 셀의 은닉상태로 입력됨과 동시에 출력층으로도 향한다.
다음 포스트에서는 LSTM을 직접 코드로 구현해볼 것이다.
참고
2) 장단기 메모리(Long Short-Term Memory, LSTM)
바닐라 아이스크림이 가장 기본적인 맛을 가진 아이스크림인 것처럼, 앞서 배운 RNN을 가장 단순한 형태의 RNN이라고 하여 바닐라 RNN(Vanilla RNN)이라고 합니다 ...
wikidocs.net
https://ko.wikipedia.org/wiki/%EC%95%84%EB%8B%A4%EB%A7%88%EB%A5%B4_%EA%B3%B1
아다마르 곱 - 위키백과, 우리 모두의 백과사전
선형대수학에서, 아다마르 곱(영어: Hadamard product)은 같은 크기의 두 행렬의 각 성분을 곱하는 연산이다. 즉, 일반 행렬곱은 m × n {\displaystyle m\times n} 과 n × p {\displaystyle n\times p} 의 꼴의 두 행렬
ko.wikipedia.org
https://ratsgo.github.io/natural%20language%20processing/2017/03/09/rnnlstm/
RNN과 LSTM을 이해해보자! · ratsgo's blog
이번 포스팅에서는 Recurrent Neural Networks(RNN)과 RNN의 일종인 Long Short-Term Memory models(LSTM)에 대해 알아보도록 하겠습니다. 우선 두 알고리즘의 개요를 간략히 언급한 뒤 foward, backward compute pass를 천천
ratsgo.github.io
'[AI] - Neural Network' 카테고리의 다른 글
| Long Short-Term Memory (LSTM) - Code (0) | 2022.01.03 |
|---|---|
| Recurrent Neural Network (RNN) - Code (0) | 2021.12.07 |
| Recurrent Neural Network (RNN) - Theory (0) | 2021.12.07 |
| Convolution Neural Network (CNN) - Code (0) | 2021.05.06 |
| Convolution Neural Network (CNN) - Theory (0) | 2021.05.03 |