이번 포스트에서는 지난 포스트에서 다루었던 RNN의 이론을 바탕으로 코드로 직접 구현해본다. RNN의 은닉층 연산에 대해 간단히 복습을 해보자.
$h_{t} = tanh(W_{x}x_{t} + W_{h}h_{t-1} + b)$
위 식은 이전 메모리 셀의 은닉 상태($h_{t-1}$)와 현재 시퀀스의 입력 데이터($x_{t}$)를 바탕으로 현재 메모리 셀의 은닉 상태를 연산하는 식을 의미한다.
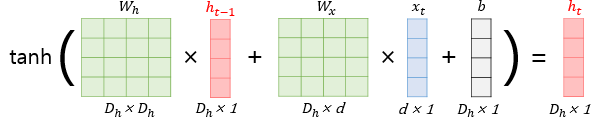
$D_{h}$ : 은닉층의 크기
$d$ : 입력 벡터의 크기 (피처 수, 단어의 종류 수)
Numpy를 통한 구현
import numpy as np
# sequence data : N x T x D (샘플 수 x 시퀀스 수 x 차원 수)
time_steps = 10 # T (시퀀스 수)
input_dim = 4 # D d (차원 수)
hidden_size = 8 # Dh (은닉층 크기)
# 샘플 수가 1이라고 가정해서 (1 x T x D)
inputs = np.random.random((time_steps, input_dim))
# 은닉 상태 (hidden state)
hidden_state_t = np.zeros((hidden_size,))
# Wx : Dh x d
Wx = np.random.random((hidden_size, input_dim))
# Wh : Dh x Dh
Wh = np.random.random((hidden_size, hidden_size))
# b : Dh x 1
b = np.random.random((hidden_size,))
total_hidden_states = []
for input_t in inputs:
# 은닉층 연산
output_t = np.tanh(np.dot(Wx, input_t) + np.dot(Wh, hidden_state_t) + b)
# 매 시퀀스마다 출력값 저장
total_hidden_states.append(list(output_t))
print(np.shape(total_hidden_states))
# 은닉 상태를 갱신
hidden_state_t = output_t
total_hidden_states = np.stack(total_hidden_states, axis=0)
print('\n', total_hidden_states.shape)
print(total_hidden_states)
Pytorch를 통한 구현
"""
두 번째 단어를 입력으로 세 번째 단어가 무엇이 나올지 예측
"""
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
sentences = ['i like dog',
'i love coffee',
'i hate milk',
'you like cat',
'you love milk',
'you hate coffee']
dtype = torch.float
# sentences에 출현하는 단어 목록
word_list = list(set(' '.join(sentences).split()))
# 각 단어에 해당하는 인덱스 매핑
word_dict = {w: i for i, w in enumerate(word_list)}
# 각 인덱스에 해당하는 단어 매핑
number_dict = {i: w for i, w in enumerate(word_list)}
# 모든 단어의 종류 수 : 9 (d)
n_class = len(word_dict)
# 문장의 수 (샘플의 수) : 6 (N)
batch_size = len(sentences)
# 은닉층 사이즈 (Dh)
n_hidden = 5
def make_batch(sentences):
input_batch = []
target_batch = []
for sentence in sentences:
# 문장을 단어로 토크나이즈
words = sentence.split()
# 각 문장의 2번째 까지의 단어의 인덱스
input_ = [word_dict[word] for word in words[:-1]]
# 각 문장의 마지막 단어의 인덱스
target_ = word_dict[words[-1]]
"""
np.eye(n_class)[[7, 0]] -> [[0. 0. 0. 0. 0. 0. 0. 1. 0.]
[1. 0. 0. 0. 0. 0. 0. 0. 0.]]
"""
input_batch.append(np.eye(n_class)[input_]) # One-Hot Encoding
target_batch.append(target_)
return input_batch, target_batch
# 텐서로 변환
input_batch, target_batch = make_batch(sentences)
input_batch = torch.tensor(input_batch, dtype=torch.float32, requires_grad=True)
target_batch = torch.tensor(target_batch, dtype=torch.int64)
print(input_batch.shape) # N x T x D : (6, 2, 9)
print(target_batch.shape) # (6,)
class TextRNN(nn.Module):
def __init__(self):
super(TextRNN, self).__init__()
self.rnn = nn.RNN(input_size=n_class, hidden_size=n_hidden, dropout=0.3)
# 최종 출력 : yt = f(Wy*ht + b)
# ht : (6, 5) / Wx : (5, 9) / b : (9,)
self.W = nn.Parameter(torch.randn([n_hidden, n_class]).type(dtype))
self.b = nn.Parameter(torch.randn([n_class]).type(dtype)) # (9,)
def forward(self, X, hidden):
# (sequence의 길이, batch 크기, input vector 사이즈) 로 input_data의 shape를 변경하여,
# mini-batch 단위의 학습이 진행 될 수 있도록 한다.
# switch dim 0 and 1 : (6, 2, 9) -> (2, 6, 9)
X = X.transpose(0, 1)
# X : (2, 6, 9), hidden : (1, 6, 5)
outputs, hidden = self.rnn(X, hidden)
# outputs : (2, 6, 5) (출력 갯수 x batch_size x n_hidden)
# outputs : (6, 5) (맨 마지막 노드의 출력)
# model : (6, 9)
outputs = outputs[-1]
model = torch.mm(outputs, self.W) + self.b
return model
model = TextRNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
for epoch in range(500):
# hidden : 초기 은닉 상태 (Dh x 1) -> 그림에서 설명한 Dh x 1 은 사실 배치 사이즈가 1이라고 가정하고 1 x Dh x 1 이다.
# 코드상으로는 배치사이즈가 6이므로 6 x 5 x 1 이지만, 양방향성 여부를 표현하면 1 x 6 x 5 x 1이 된다.
# 양방향일시 zeros(2, ..)
hidden = torch.zeros(1, batch_size, n_hidden, requires_grad=True)
output = model(input_batch, hidden) # input_batch : (6, 2, 9), hidden : (1, 6, 5)
loss = criterion(output, target_batch) # output : (6, 9), target_batch : (6,)
if (epoch + 1) % 100 == 0:
print('Epoch : ', '%04d' % (epoch + 1), 'Cost : ', '{:.6f}'.format(loss))
optimizer.zero_grad()
loss.backward()
optimizer.step()
hidden = torch.zeros(1, batch_size, n_hidden, requires_grad=True)
predict = model(input_batch, hidden).data # (6, 9)
predict = predict.max(axis=1, keepdim=True)[1] # (6, 1)
print([number_dict[n.item()] for n in predict.squeeze()])
# [참고] torch.Tensor.max
a = torch.randn(3, 4)
print(a)
"""
tensor([[ 0.7745, -1.2034, 0.7053, 0.0947],
[ 1.3365, -0.0998, -0.0091, 0.1973],
[-0.1648, 0.9201, 0.8369, 0.2715]])
"""
print(torch.max(a, axis=0))
"""
torch.return_types.max(
values=tensor([1.3365, 0.9201, 0.8369, 0.2715]),
indices=tensor([1, 2, 2, 2]))
"""
참고
1) 순환 신경망(Recurrent Neural Network, RNN)
RNN(Recurrent Neural Network)은 시퀀스(Sequence) 모델입니다. 입력과 출력을 시퀀스 단위로 처리하는 모델입니다. 번역기를 생각해보면 입력은 번 ...
wikidocs.net
https://justkode.kr/deep-learning/pytorch-rnn
Pytorch로 RNN, LSTM 구현하기
Pytorch 에서는 CNN과 마찬가지로, RNN과 관련 된 API를 제공합니다. 이를 이용해 손쉽게 RNN 네트워크를 구축 할 수 있습니다. Recurrent Neural Network RNN (Recurrent Neural Network)를 위한 API는 torch
justkode.kr
'[AI] - Neural Network' 카테고리의 다른 글
| Long Short-Term Memory (LSTM) - Code (0) | 2022.01.03 |
|---|---|
| Long Short-Term Memory (LSTM) - Theory (0) | 2021.12.09 |
| Recurrent Neural Network (RNN) - Theory (0) | 2021.12.07 |
| Convolution Neural Network (CNN) - Code (0) | 2021.05.06 |
| Convolution Neural Network (CNN) - Theory (0) | 2021.05.03 |