이번 포스트에서는 합성곱(Convolution) 연산을 기반으로 이미지에서 특징을 검출하는데에 적합한 신경망인 CNN에 대해 알아본다. 먼저 CNN의 전체적인 구조에 대해 살펴보자.

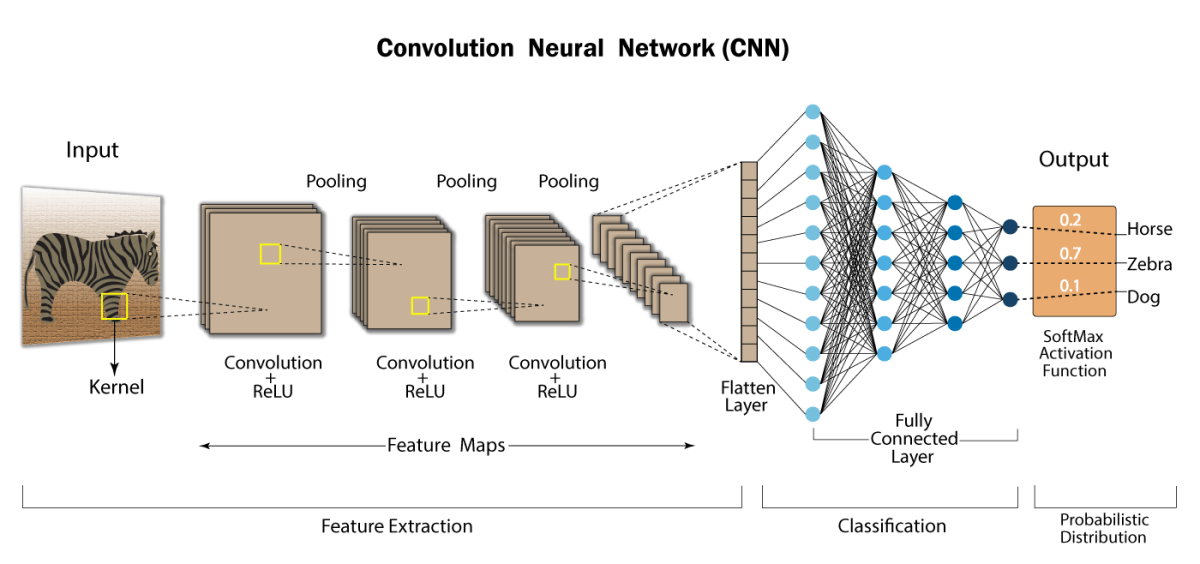
Input으로 이미지가 들어오면 Convolution, Activation function, Pooling 세 가지의 레이어가 반복적으로 나타난다. 이 과정은 이미지로부터 작은 특징들부터 조합하여 점점 큰 특징들을 검출하는 과정이다. 그 후에는 Flatten 과정을 통해 검출한 특징들에 대한 이미지(feature map)를 일렬로 펼치는 작업을 수행한다. 마지막으로 Fully Connected 레이어를 통해 모든 클래스에 대해 일치할 확률을 출력한다.
CNN의 구조에 나오는 기본용어에 대해서 간략하게 정리해보자. 그전에, 이미지는 텐서로 이루어져 있다는 것을 알았으면 좋겠다. RGB 이미지일경우 3채널(R채널, G채널, B채널)로 구성되어 있다. 예를 들어, 256 x 256 RGB 이미지가 있다고 가정하면 해당 이미지는 (256 x 256 x 3) 형태의 텐서다.
Feature
Feature는 특징이라는 의미로, 우리가 이미지로부터 검출할 특징을 의미한다. CNN에서 Feature는 각 픽셀을 의미한다.
Weight
Weight는 가중치라는 의미로, 각각의 특징(Feature)이 갖는 중요도를 의미한다. 예를들어, 고양이를 판별하기 위한 특징으로 "귀가 뾰족함", "코가 세모"라는 두 가지 특징이 있다고 가정할 때, 귀의 모양을 더 중점적으로 본다면 "귀가 뾰족함"이라는 특징은 0.6, "코가 세모"라는 특징은 0.4로 계산할 수 있다.
Kernel (Filter)

커널 혹은 필터는 이미지로부터 특징을 검출하기 위한 단위 영역이다. 동시에 Weight의 집합이다(각각의 요소가 가중치). 이 영역은 보통 정사각형 (N x N) 형태이며, 넓을수록 (N이 클수록) 더욱 넓은 영역을 보기때문에 추상적인 개념을, 좁을수록 더 작은 영역을 바라본다.
커널의 갯수가 많을수록 다양한 특징을 이미지로 부터 검출할 수 있다. 이렇게 여러 커널로 인해 이미지로부터 검출된 특징들의 집합을 다중 특징맵 (multiple feature map)이라고 한다.
+ Traditional Kernel과 다른점 (중요)

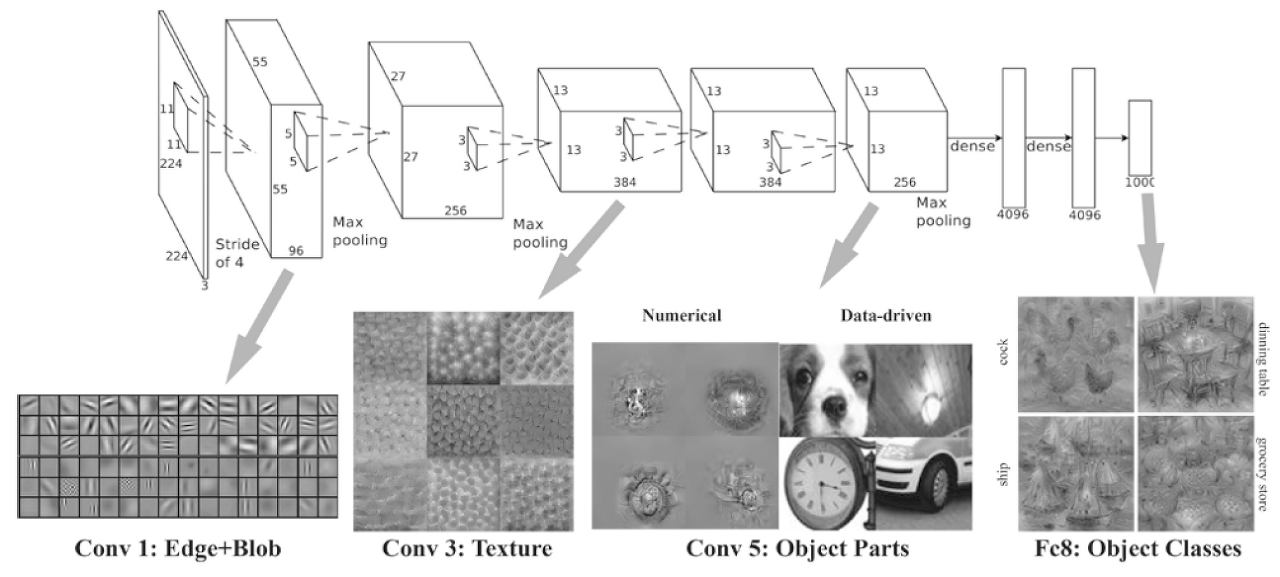
전통적인 비전 영역에서는 이미지에서 특징을 검출하기 위한 필터를 사람이 직접 설계(design)했다. 위 이미지에서 Classic Machine Learning에 속한다고 볼 수 있다. (Hand-designed features) 하지만, 딥러닝의 영역에서는 이러한 feature를 사람이 아닌 기계가 자동으로 찾아주는 역할을 하게 되는 것이 관건이다. 즉, 검출하려는 특징과 일치하는 필터(가중치)를 Backpropagation을 통해 학습하여 찾아내는 것이다.
Convolution (합성곱)
합성곱이라 하면 필자는 벡터의 내적 연산을 생각한다. 두 벡터 사이의 요소들의 곱을 합한 것을 말한다.
ex)
v1 = (1, 2, 3)
v2 = (2, 3, 4)
v1 @ v2 = 1차원의 곱 (1 * 2) + 2차원의 곱 (2 * 3) + 3차원의 곱 (3* 4) = 2 + 6 + 12 = 20
3차원 벡터 v1, v2가 있다고 가정할 때 같은 차원끼리 곱을 의미한다. 벡터의 연산의 산출물은 스칼라(값)이다.

위 그림과 같이 [[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]] 형태의 3 x 3 커널이 있다고 가정할 때, 보라색 특정영역에 합성곱을 진행하면 각 위치의 곱에 대해 합을 진행하면 21이 나온다. 여기서 주의해야 할 점이 있다.
합성곱 연산을 수행하면 이미지의 크기가 줄어든다는 점이다.
+ MLP (Multi Layer Perceptron)과의 차별성 (중요)

MLP의 FC(Fully-Connected)속성에 의해 각 픽셀은 모든 출력과 연결되어 있어 가중치가 많다. 반면, CNN은 필터(가중치)라는 개념을 사용하기 때문에 지역성(locality)를 고려할 수도 있고, 가중치가 획기적으로 적은 것을 알 수 있다.
Padding

원래는 노란색으로 칠한 영역은 존재하지 않지만, 합성곱 연산으로 인해 줄어든 이미지(정확히는 출력 텐서)의 크기를 동일하게 유지하기 위해 임의의 값으로 padding(채우기)를 해준다.
Stride

Stride는 보폭이라는 의미로, 커널이 이미지의 특정 영역에 대해 Convolution 연산을 수행한 뒤, 몇칸만큼 이동할 것인지를 의미한다. 위 그림에서 빨간색 영역에서 연산을 진행한 뒤, 파란색 영역으로 이동하면 1칸 이동한 것이므로 Stride는 1이다.
Activation Function

해석하자면 활성함수를 의미한다. 실은 퍼셉트론이라는 개념을 알고있으면 훨씬 이해하기 쉽다. 퍼셉트론은 사람의 신경세포(뉴런)을 프로그래밍화 시켜놓은 것이다. 뉴런은 특정 신호들을 입력으로 받아 나온 결과값이 특정 임계치를 넘으면 신호가 발생하고 그렇지 않으면 발생하지 않는다. 이는 퍼셉트론도 마찬가지다. 퍼셉트론에서 입력받은 신호는 이전 레이어에서 입력받은 결과이다. 그리고, 이를 합성곱 연산을 통해 나온 값에 임계치를 적용해야 하는데 이 임계치가 Activation Function이다. 대표적인 종류로는 Tanh, Sigmoid, ReLU, LeakyReLU 등이 있다.
+ ReLU를 선호하는 이유 (중요)

Sigmoid의 경우에는 Gradient Vanishing 현상이 고질적으로 발생한다. 그 이유는 크게 두 가지이다. 첫 번째 이유는 Sigmoid의 출력값 자체가 0과 1사이에 수렴하기 때문이다. 즉, 아무리 커도 1보다 작은 값인데, 레이어가 깊어질수록 점점 작은 값을 곱하게 되면 결국 신호 자체는 사라져 버린다. 두 번째 이유는 Backpropagation에서 알 수 있다. 편미분을 하는 Backpropagation 특성상 Sigmoid 함수의 미분결과(즉, 기울기)가 0인 지점이 존재하기 때문이다.

하지만 ReLU는 단순하면서도 미분의 결과가 0인 지점을 제거했기 때문이다. 추가로, 비전 영역에서 ReLU를 선호하는 이유는 Segmentation의 효과도 있다고 한다. (인식한 객체 이외의 Background는 0으로 수렴시키기 때문)
Pooling

pooling 연산은 데이터를 압축시키기 위한 개념이다. 예를들어 위 그림처럼 pooling의 stride를 2로 주었을 때, max pooling (이외에도 여러가지 풀링연산이 있음)을 하였을 때, 가장 높은 특징값만 도출해낸다. 위 그림에서는 14에 해당한다. pooling 연산을 수행하는 목적은 주된 특징만 강조시켜 학습시키기 위한 파라미터(가중치)를 줄이기 위함이다.
Flatten

CNN의 모든 Convolution layers를 거치고 Fully Connected layers를 거치기 전에 여러 차원의 텐서를 일렬로 펼치는 작업이다. 이를 대체할 수 있는 수단인 GAP (Global Average Pooling)이 Network In Network 논문에서 처음으로 소개되기도 했다.
Fully Connected layers
Flatten 과정을 통해 일렬로 펼친 텐서를 원하는 채널 수만큼 완전 연결하는 과정이다. 위 그림에서는 11 -> 7 -> 5 -> 3 으로 완전 연결이 되어 있다. Fully Connected layers를 전부 통과하고나면 분류하고자 하는 클래스의 수만큼 값이 나와야 한다.
개념은 이정도로 마치고 다음 포스트에서는 코드를 통해 직접 이해해보는 시간을 가져보도록 하겠다.
'[AI] - Neural Network' 카테고리의 다른 글
| Long Short-Term Memory (LSTM) - Theory (0) | 2021.12.09 |
|---|---|
| Recurrent Neural Network (RNN) - Code (0) | 2021.12.07 |
| Recurrent Neural Network (RNN) - Theory (0) | 2021.12.07 |
| Convolution Neural Network (CNN) - Code (0) | 2021.05.06 |
| ILSVRC 2012 Dataset (0) | 2021.04.29 |