열 공간 (Column Space)

이론

행렬 A의 열 벡터들에 대한 가능한 모든 선형 조합(Ax)의 결과를 모아 집합으로 구성할 수 있을 것이다. 이를 집합을  열 공간이라고 한다.

 

열 공간은 다음과 같이 표기한다.

 

 

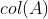
- Consistent Linear System

선형 시스템 Ax = b가 해를 가지면 다음을 만족한다.

 

 

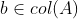
- Inconsistent Linear System

선형 시스템 Ax = b의 해가 없으면 다음을 만족한다.

 

 

 

위의 행렬의 열 공간은 3차원 공간이다. 세 개의 열 벡터가 존재하기 때문에 3가지 방향으로 갈 수 있기 때문이다.

 

 

따라서, 어떤 3-벡터 b를 이용해 선형 시스 Ax = b를 구성한다고 하더라도, 해당 선형 시스템의 해는 존재한다. (Consistent Linear System)

 

 

반면 위 행렬의 열 공간은 xy-평면이다. 그 이유는 세 개의 열 벡터가 z값이 0이기 때문이다.

 

위와 같은 열 공간은 b가 xy-평면 상에 존재해야만 해가 존재할 수 있다.

 

z값이 0인 열 벡터의 집합

 

 

3-벡터 b가 xy-평면상에 높여있을 경우에만 해가 존재한다.