이번 포스트에서는 행렬의 간단한 표기법들과 종류, 연산들에 대해 알아볼 예정이다.
이론
행렬의 표기법
m x n 행렬은 다음과 같이 표기한다.

그리고 행렬의 i번째 행의 j번째 열의 요소는 다음과 같이 표기한다.

행렬의 종류
- 전치 행렬 (Transpose Matrix)
전치행렬은 특정행렬의 행과 열을 바꾼 행렬이다. i번째 행의 j번째 열의 요소는 j번째 행의 i번째 열의 요소와 자리가 바뀐다.
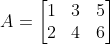
위와 같은 행렬이 존재한다고 가정하자. A의 전치행렬은 다음과 같다.

- 영 행렬 (Zero Matrix)
모든 요소가 0으로 이루어진 행렬을 의미한다.
영 행렬은 행렬 덧셈 연산에 대한 항등원 역할을 한다.

- 정방 행렬 (Square Matrix)
행과 열의 갯수가 동일한 행렬을 의미한다.

- 항등 행렬 (Identity Matrix)
주 대각선의 모든 요소가 1, 그 밖의 요소는 전부 0인 n차 정방 행렬을 의미한다.
항등 행렬은 행렬 곱셈 연산에 대한 항등원 역할을 한다.
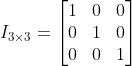
행렬의 연산
- 행렬의 곱
행렬 C의 각 요소는 행렬 A의 i번째 행 벡터와 행렬 B의 j번째 열 벡터의 내적(inner product)이다. 행렬의 곱은 병렬처리로 가속화할 수 있다.


코드
import numpy as np
A = np.array([[1, 3, 5],
[2, 4, 6]])
print(A.shape) # (2, 3)
# 전치 행렬 (Transpose)
t = A.T
print(t, t.shape)
>>
[[1 2]
[3 4]
[5 6]] (3, 2)
# 영 행렬 (Zero)
z = np.zeros((3, 3))
print(z)
>>
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
# 항등 행렬 (Identity)
i = np.eye(3)
print(i)
>>
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
# 행렬의 곱셈
print(A @ t)
print(np.matmul(A, t))
>>
[[35 44]
[44 56]]
[[35 44]
[44 56]]'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| 열 공간 (Column Space) (0) | 2021.06.20 |
|---|---|
| 선형 조합 (Linear Combination) (0) | 2021.06.18 |
| LU 분해 (LU Decomposition) (0) | 2021.06.13 |
| 가우스 소거법 (Gauss Elimination) (0) | 2021.06.10 |
| 선형 시스템 (Linear System) (0) | 2021.06.10 |