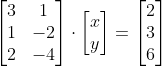이론
중고등학교때 다들 '함수'라는 개념은 익히 알고있을 것이다. 함수는 방정식으로써 표현이 가능하고, 미지수가 적을 경우 수기로도 충분히 해를 구할 수 있다. 하지만, 방대한 양의 데이터들의 상관관계를 수학으로 표현하기란 쉽지 않다.
우리는 이러한 상관관계를 파악하고 해를 구하기 위해 선형 시스템이라는 개념을 숙지해야 한다. 선형 시스템이란 선형 방정식 (Linear Equation)들의 집합이다. 선형 방정식은 말 그대로 직선형태의 함수 즉, 1차 함수 방정식을 의미한다.
예를 들어보자.
$3x + y + z = 4$
$x - 2y - z = 1$
$x + y + z = 2$
다음과 같이 세 가지 방정식이 있다. 각각의 방정식은 Linear Equation이 된다. 그리고 미지수(Unknow, Variable)는 총 3가지(x, y, z)가 있다. 이처럼 3개의 선형 방정식과 3개의 미지수로 구성되어 있으면 3 x 3 선형 시스템이라고 표현한다.
우리는 선형 시스템을 효율적으로 해결하기 위해서는 대수적으로 표현할 필요가 있다.
위 선형 시스템을 대수적으로 표현하면 다음과 같다.

우리는 해당 선형 시스템에 대한 해인 $x$, $y$, $z$를 구하기 위해서 행렬 A의 역행렬을 양변에 곱하면 된다.

코드
import numpy as np
import numpy.linalg as lin
# 선형 시스템 A
A = np.array([[3, 1, 1],
[1, -2, -1],
[1, 1, 1]])
b = np.array([4, 1, 2])
# A의 역행렬
A_inv = lin.inv(A)
# 해
x = np.matmul(A_inv, b)
print(x)
>>
[ 1. -1. 2.]
참고
https://rfriend.tistory.com/380
[Python NumPy] 선형대수 함수 (Linear Algebra)
학교 다닐 때 행렬로 연립방정식 풀었던 기억이 날 듯 합니다. 선형대수(Linear Algebra)는 통계, 기계학습, 공학, 영상/이미지 처리 등 여러 분야에서 활용이 됩니다. 선형대수를 전부 다루려면 너
rfriend.tistory.com
'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| 열 공간 (Column Space) (0) | 2021.06.20 |
|---|---|
| 선형 조합 (Linear Combination) (0) | 2021.06.18 |
| 행렬 연산 (Matrix Operations) (0) | 2021.06.18 |
| LU 분해 (LU Decomposition) (0) | 2021.06.13 |
| 가우스 소거법 (Gauss Elimination) (0) | 2021.06.10 |