https://dev-ryuon.tistory.com/45
# 0. 선형 시스템 (Linear System)
[이론] 중고등학교때 다들 '함수'라는 개념은 익히 알고있을 것이다. 함수는 방정식으로써 표현이 가능하고, 미지수가 적을 경우 수기로도 충분히 해를 구할 수 있다. 하지만, 방대한 양의 데이
dev-ryuon.tistory.com
이 포스트는 선형 시스템에 대해 숙지하고 보시는 것을 추천합니다.
이론
선형 시스템은 해를 가지는 케이스가 총 3가지로 나누어진다.
1. 해가 하나인 경우 - x=2 인경우에만 성립한다.
ex) 3x = 6
2. 해가 여러개인 경우 - 어떠한 x를 대입하더라도 성사된다.
ex) 0x = 0
3. 해가 존재하지 않는 경우 - 어떠한 x를 대입하더라도 성사되지 않는다.
ex) 0x = 6
1, 2번과 같이 해가 존재하는 경우를 consistent 하다고 표현한다. 반면 해가 존재하지 않는 경우는 inconsistent 하다고 표현한다.
.
.
.
본격적으로 가우스 소거법에 대한 이야기를 시작하겠다. 가우스 소거법은 선형 시스템의 해를 구하는 대표적인 방법이다. 우리가 선형 시스템을 보자마자 바로 해를 구할 수 없는 이유는 무엇일까? 그 이유는 바로 행렬 A의 원소수가 너무 많기 때문이다. 가우스 소거법은 행렬 A를 해를 구하기 쉽게 원소들을 소거하는 과정이다.
가우스 소거법은 크게 두 단계로 진행된다.
1. 전방 소거법 (Foward Elimination)
2. 후방 대입법 (Back Substitution)

먼저 위와 같은 선형 시스템이 있다고 가정하자. $*$은 임의의 값(동일하지 않은 랜덤값)을 의미한다. 위와 같은 형태에서는 $x$, $y$, $z$를 바로 알기 어려울 것이다.
그러나, 전방 소거법을 마친 형태는 다음과 같다.

$(0 \times x) + (0 \times y) + (* \times z) = c$
$z = c / *$
전방 소거법을 마쳤으면 후방 대입법을 진행할 차례이다. A 행렬의 가장 마지막 3번째 행부터 행렬곱을 진행하면 위 식과 같다.
$(0 \times x) + (* \times y) + (* \times z) = b$
2번째 행의 연산은 위 식과 같다. 우리는 이미 z가 무엇인지 파악했기 때문에 그대로 대입하고 $y$만 구하면 된다.
$(* \times x) + (* \times y) + (* \times z) = a$
마찬가지로 1번째 행렬곱에서는 위 식과 같다. 위에서 $y$, $z$를 이미 구했다. 그대로 대입하고 $x$만 구하면 된다.
.
.
.
그렇다면.. 전방 소거법은 어떻게 이루어지는지 파악할 필요가 있다.
전방 소거법은 주대각선의 요소가 전부 1이 되어야 한다.
전방 소거법은 기본 행 연산 (ERO : Elementary Row Operations)을 기반으로 이루어진다.
기본 행 연산은 크게 3가지로 구성된다.
1. Interchange (교환 : $R_{ij}$) : $i$번째 행과 $j$번째 행을 서로 교환한다.
2. Scaling (스케일링 : $R_{i}(c)$) : $i$번째 행에 0이 아닌 상수 c를 곱한다.
3. Replacement (치환 : $R_{ij}(c)$) : $i$번째 행에 상수 c를 곱한 뒤, j번째 행과 더한다.

위와 같은 선형 시스템이 있다고 가정하고 실제로 전방 소거법을 진행해보겠다.
$R_{12}(-1) : r_2 = r_2 + (-1) \times r_1$
먼저 1번행과 2번행에 대한 치환 연산을 수행한다. 두 번째 방정식 $1x_{1} + 2x_{2} + 3x_{3} = 3$에 첫 번째 방정식 $1x_{1} + 2x_{2} + 1x_{3} = 1$을 빼는 것과 동일하다. ($2x_{3} = 2$가 되겠죠?)

$R_{13}(-2) : r_3 = r_3 + (-2) \times r_1$
그 다음 1번 행과 3번행에 대한 치환 연산을 수행한다.

$R_{23} : r2 <-> r3$
그 다음 2행 2열(주대각선 원소중 하나)의 값이 0이므로 1로 맞추기 위해 2번 행과 3번행에 대한 교환 연산을 수행한다.
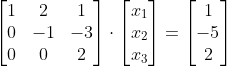
$R_{2}(-1) : r2 \times (-1)$
$R_{3}(1/2) : r3 \times (1/2)$
마지막으로 주대각선의 원소들을 1로 맞추기 위해 2행과 3행에 스케일링 연산을 수행한다.

.
.
.
후방 대입법은..
$x_{3} = 1$
$x_{2} + 3x_{3} = x_{2} + 3 = 5$
$x_{2} = 2$
$x_{1} + 2x_{2} + x_{3} = x_{1} + 4 + 1 = 1$
$x_{1} = -4$
열벡터(해)는 다음과 같이 구할 수 있다.

.
.
.
전방 소거법은 다음과 같은 가치를 지닌다.
- 주어진 선형 시스템을 가장 풀기 쉬운 형태로 변형해준다.
- 주어진 선형 시스템의 rank를 알려준다. (실질적으로 존재하는 방정식의 갯수)
- 선형 시스템에 해가 있는지 (consistent) 없는지 (inconsistent) 알려준다.
코드
import numpy as np
import numpy.linalg as lin
# 4x_{1} + 3x_{2} = 23
# 3x_{1} + 2x_{2} = 16
# 두 방정식의 해
a = np.array([[4, 3],
[3, 2]])
b = np.array([23, 16])
x = lin.solve(a, b)
print(x)
>>
[2. 5.]import numpy as np
import numpy.linalg as lin
A = np.array([[1, 2, 1],
[1, 2, 3],
[2, 3, -1]])
# 행렬의 rank 계산 - 실질적으로 존재하는 방정식의 수
rank_A = lin.matrix_rank(A)
print(rank_A)
B = np.array([[1, 2, 1],
[1, 2, 3],
[2, 4, 6]])
# [1, 2, 3] -> 1x_{1} + 2x_{2} + 3x_{3}
# [2, 4, 6] -> 2x_{1} + 4x_{4} + 6x_[3]
# 두 방정식은 동일
rank_B = lin.matrix_rank(B)
print(rank_B)
>>
3
2'[Mathematics] - Linear Algebra' 카테고리의 다른 글
| 열 공간 (Column Space) (0) | 2021.06.20 |
|---|---|
| 선형 조합 (Linear Combination) (0) | 2021.06.18 |
| 행렬 연산 (Matrix Operations) (0) | 2021.06.18 |
| LU 분해 (LU Decomposition) (0) | 2021.06.13 |
| 선형 시스템 (Linear System) (0) | 2021.06.10 |