이번 포스트에서는 저번 포스트에서 다루었던 군집화 알고리즘이 잘 수행되었는지 판단하기 위한 지표에 대해 알아본다. 이번에 알아볼 지표로는 두 가지로 실루엣 계수와 응집도가 있다.
실루엣 계수 (silhouette score)


실루엣 계수는 각각의 데이터가 해당 데이터와 같은 군집 내의 데이터와는 얼마나 가깝게 군집화가 되었고, 다른 군집에 있는 데이터와는 얼마나 멀리 분포되어 있는지를 나타내는 지표이다. 실루엣 계수가 가질 수 있는 값은 -1~1이며, 1에 가까울수록 군집화가 잘 되었음을 의미한다.
하지만, 데이터 하나에 대한 실루엣 계수만 좋다고 군집화가 잘 이루어졌다고 일반화를 할 수 없다. 각 군집별 데이터의 수가 고르게 분포되어야 하며, 각 군집별 실루엣 계수 평균값이 전체 실루엣 계수 평균값에 크게 벗어나지 않는 것이 중요하다.

위 그림은 군집별로 실루엣 계수를 시각화한 예시이다. 빨간 점선은 전체 실루엣 계수의 평균을 의미한다. 어떠한 군집화가 잘 이루어졌는지 판단해보자.
군집 갯수 = 2, 평균 실루엣 계수 0.705
군집별 실루엣 계수 평균값이 0보다 크고 편차가 크지 않지만, 두 군집의 데이터 수의 차이가 많다.
군집 갯수 = 3, 평균 실루엣 계수 0.588
2번 군집에 실루엣 계수가 음수인 데이터들이 존재한다. 이는 2번 군집의 실루엣 계수와 전체 실루엣 계수에 편차가 큰 것을 의미한다.
군집 갯수 = 4, 평균 실루엣 계수 0.651
모든 군집의 데이터 수의 비율이 고른 편이고, 실루엣 계수가 음수인 데이터들도 존재하지 않으므로 최적의 군집화 결과로 판단된다.
import math
import matplotlib.cm as cm
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
def visualize_silhouette(cluster_lists, X_features):
# 입력값으로 클러스터링 갯수들을 리스트로 받아서, 각 갯수별로 클러스터링을 적용하고 실루엣 개수를 구함
n_cols = len(cluster_lists)
# plt.subplots()으로 리스트에 기재된 클러스터링 수만큼의 sub figures를 가지는 axs 생성
fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)
# 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 실루엣 개수 시각화
for ind, n_cluster in enumerate(cluster_lists):
# KMeans 클러스터링 수행하고, 실루엣 스코어와 개별 데이터의 실루엣 값 계산.
clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
cluster_labels = clusterer.fit_predict(X_features)
sil_avg = silhouette_score(X_features, cluster_labels)
sil_values = silhouette_samples(X_features, cluster_labels)
y_lower = 10
axs[ind].set_title('Number of Cluster : '+ str(n_cluster)+'\n' \
'Silhouette Score :' + str(round(sil_avg,3)) )
axs[ind].set_xlabel("The silhouette coefficient values")
axs[ind].set_ylabel("Cluster label")
axs[ind].set_xlim([-0.1, 1])
axs[ind].set_ylim([0, len(X_features) + (n_cluster + 1) * 10])
axs[ind].set_yticks([]) # Clear the yaxis labels / ticks
axs[ind].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
# 클러스터링 갯수별로 fill_betweenx( )형태의 막대 그래프 표현.
for i in range(n_cluster):
ith_cluster_sil_values = sil_values[cluster_labels==i]
ith_cluster_sil_values.sort()
size_cluster_i = ith_cluster_sil_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_cluster)
axs[ind].fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_sil_values, \
facecolor=color, edgecolor=color, alpha=0.7)
axs[ind].text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
axs[ind].axvline(x=sil_avg, color="red", linestyle="--")from sklearn.datasets import load_iris
iris = load_iris()
visualize_silhouette([2, 3, 4, 5], iris.data)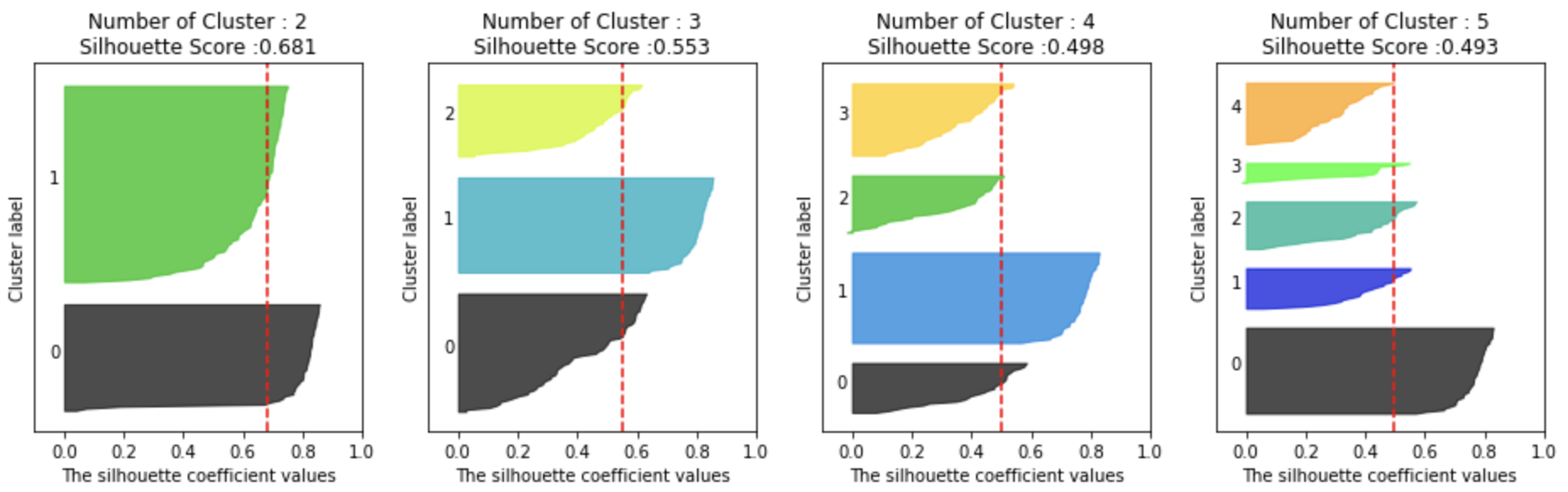
위 그림은 군집의 갯수별로 붓꽃 데이터의 실루엣 계수를 시각화한 것이다. 위에서 군집화가 잘 된 예시를 통해 몇 번 군집이 잘 되었는지를 판단하여 댓글을 남겨주면 좋을것 같다.
응집도 (Inertia)
응집도는 각 군집별 중심점으로부터 개별 데이터와의 거리의 제곱의 합으로 이루어져 있다.


$x_i$는 i번째 데이터 즉, 개별 데이터를 의미한다. $\mu_k$는 k번째 클러스터의 중심이다. $w^{(i, k)}$는 $x_i$가 k번째 클러스터에 속하는 경우 1, 그렇지 않은 경우 0으로 정의된다. 즉, 각 군집별 데이터들의 중심점과의 편차 제곱 합(각 군집별 분산)을 모든 군집별로 합한 값이다.
군집의 갯수가 늘어날수록 각 군집별 데이터의 수가 줄어들기 때문에 일반적으로는 inertia는 감소한다. (0으로 수렴한다.) 하지만, 무조건 inertia가 작다고 좋은 것은 아니기 때문에 어떻게 좋은 군집화가 이루어졌는지 판단해보자.
import seaborn as sns
def visualize_inertia(cluster_lists, X_features):
inertias = []
for n_cluster in cluster_lists:
k_means = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
k_means.fit(X_features)
inertias.append(k_means.inertia_)
sns.lineplot(x=cluster_lists, y=inertias)visualize_inertia([i for i in range(2, 11)], iris.data)
위 그림은 군집의 갯수별로 inertia를 시각화한 그래프이다. 특정 군집 이상으로 갯수를 늘려도 inertia가 감소하는 속도가 줄어드는 시점이 있다. (위 그림에서는 3 혹은 4가 될 것이다.) 이후로는 이미 0에 수렴해가고 있기 때문에 큰 의미가 없다. 이렇게 꺾이는 모양때문에 inertia를 통한 방법은 elbow method라고도 불린다.
'[AI] - Machine Learning' 카테고리의 다른 글
| 비선형성 (Nonlinearity) (0) | 2023.06.14 |
|---|---|
| 군집화 알고리즘 (K-Means Clustering) (0) | 2021.12.09 |
| 군집화 알고리즘 (Clustering Algorithm) (0) | 2021.12.06 |
| 선형 분류 (Linear Classification) (0) | 2021.12.03 |
| 회귀 알고리즘 (Ridge, Lasso, ElasticNet) (0) | 2021.11.30 |