지난 포스트에서 선형 분류에 대해 자세히 다루지 못한것 같아 이번에 좀 자세히 다루려고 한다. 복습을 간단하게 하자면, 지도 학습에는 크게 분류와 회귀 문제가 존재한다. 그리고 회귀 문제는 데이터들을 가장 잘 나타내는 선을 찾는 것이 목적이다. 분류 문제도 회귀 문제와 메커니즘은 비슷하지만, 찾고자 하는 선의 목적이 다르다. 분류는 데이터들을 가장 잘 분류하는 선을 찾는 것이 목적이다. 즉, 회귀의 선은 데이터들 사이의 거리가 가까운 선을 찾으려고 하지만, 분류는 (클래스별로)거리가 먼 것을 찾으려고 하는 것이다.

사실 위의 그림을 이해를 위해 선으로 표현했지만, 선형 분류의 의미를 엄밀히 말하면 데이터를 잘 분류할 수 있는 초평면(hyperplane)을 찾는 것이라고 해야 정확한 의미이다.
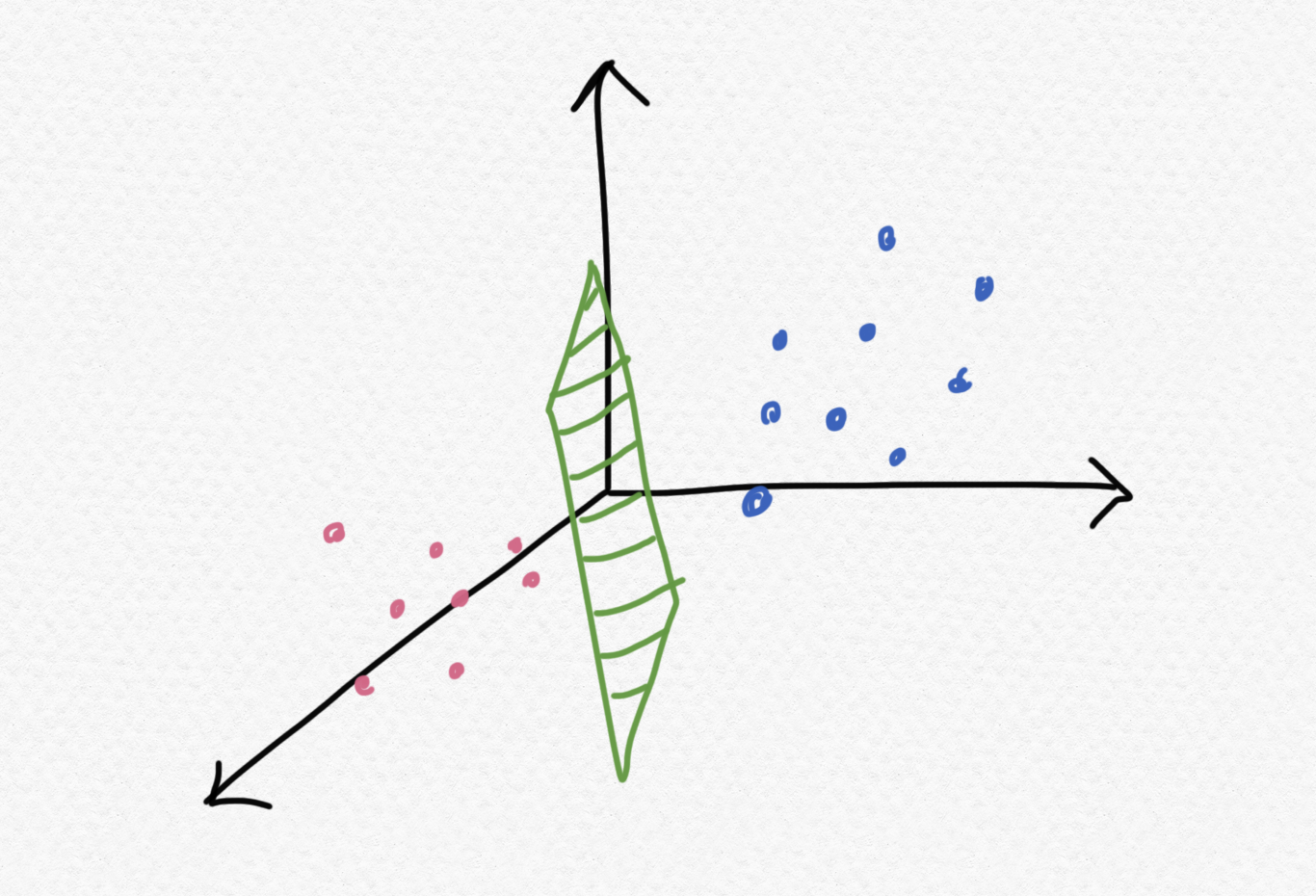
이번 포스트에서는 분류에 대해 다룰 예정이다. 분류는 크게 이진 분류와 다중 분류로 나눌 수 있다. 먼저 이진 분류부터 알아보자.
[이진 분류]
이진 분류는 특정 벡터(데이터)가 2개의 클래스 중 어떤 클래스에 속하는지를 찾는 문제이다. 예를 들면, 2개의 클래스가 강아지와 고양이라고 가정하자. 특정 이미지(이미지는 행렬이자, 벡터들의 집합)를 입력으로 주었을 때, 강아지일 확률이 0.7일 경우, 0.5보다 큰 값을 지니므로 강아지로 판별한다. (70% 확률로 강아지, 30% 확률로 고양이)
P.S) 이진 분류는 로지스틱 회귀라고도 한다.
먼저 분류 문제 또한 선을 찾기 위한 문제이기 때문에 다음과 같이 식을 정의할 수 있다.
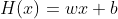
하지만, 분류를 위해 작용하는 독립 변수 (원인 혹은 feature)가 하나만 존재하리란 법은 없다. 독립 변수가 여러개라면 다음과 같이 행렬을 이용하여 정의해야 한다.
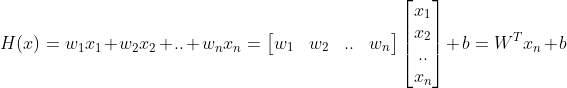
그러나 궁극적으로 우리가 분류 문제에서 얻어야 하는 결론은 특정 클래스에 속할 확률이기 때문에 0과 1 사이의 값으로 표현해주어야 한다. 0과 1사이의 값으로 표현하기 가장 적절한 비선형 함수는 시그모이드 함수 (Sigmoid function)이다.
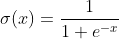
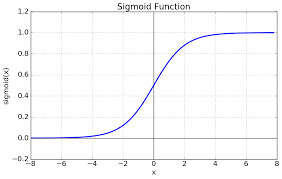
시그모이드 함수는 X=(-inf, inf) 전체 구간에서 0과 1에 사이의 값을 지닌다. 그리고, 1과 0에 정확히 도달하는 것이 아닌 수렴하는 값을 지닌다. X가 0일때는 0.5의 값을 갖는다.

우리가 최종적으로 원하는 형태는 다음과 같다. H(x)를 시그모이드 함수의 정의역에 대입하면 분류하고자 하는 클래스에 대한 확률값을 도출해낼 수 있다.
마지막으로 시그모이드를 통해 나온 값이 어느 정도 오차가 있는지 판단하기 위한 지표로 이진 교차 엔트로피(Binary Cross Entropy)를 사용한다. 교차 엔트로피 손실함수를 사용하는 이유는 회귀에서 사용한 손실 함수인 RSS나 MSE같은 것들을 사용하는 경우 오차가 아무리 커봤자 1이기 때문이다. (residual = 실제값 - 예측값 = 1 - 0)

교차 엔트로피의 식은 다음과 같다. 위 식을 분석해보자면, -1/n ∑는 각 데이터들의 오차의 평균을 구하기 위함이다. 우리가 중점적으로 보아야 할 것은 + 를 기준으로 좌항과 우항을 봐야한다. 만약 i번째 데이터의 정답(yi)이 1이라면 좌항의 yi*log(t)만이 남을 것이고, 우항은 0이 될 것이다. 반대로 i번째 데이터의 정답이 0이라면 좌항은 0이 되고, 우항의 log(1-t)만이 남을 것이다. 이 log들이 엔트로피이다.
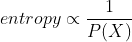
여기서 우리가 중점적으로 보아야할 것은 (정보)엔트로피이다. 엔트로피는 확률적으로 발생하는 사건에 대한 정보량(깜놀도라고 표현한다..)을 의미한다. 즉, 어떤 사건이 발생할 확률이 낮을수록 엔트로피는 높아진다. 이게 무슨 소리냐면, 발생할 확률이 낮은 사건이 발생하면 우리는 놀랄만한 정보량이 많다고 여긴다. 그래서 사건이 발생할 확률과 엔트로피는 반비례한다.


통계학에서는 정보량을 다음과 같이 정의한다. 정보량과 사건사이에는 반비례 관계를 가져야 하므로 사건이 발생할 확률 P(X)에 log를 취한 뒤에 음의 부호를 취한다.

우리는 데이터가 한 개라고 가정하고 교차 엔트로피 식을 적용하면 ∑를 제외하고 다음과 같이 정의할 수 있다.
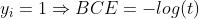
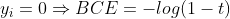
본론으로 돌아오면, ∑ 안의 항의 모든 케이스에 대해 알아보자.
1) yi가 1, t가 0.7인 경우 : 실제 정답이 1이고, 특정 클래스일 확률이 0.7이므로 log(0.7)=-0.15, 교차 엔트로피는 0.15가 된다.
2) yi가 0, t가 0.7인 경우 : 실제 정답이 0이고, 특정 클래스일 확률이 0.7이므로 log(1-t)=log(0.3)=-0.52, 교차 엔트로피는 0.52가 된다.
결론 : 실제 정답과 특정 클래스일 확률과의 오차가 커질수록 교차 엔트로피도 증가한다.
[다중 분류]
그러나 사실 클래스를 2개 이상을 분류하는 경우도 많다. 이러한 경우에는 데이터가 어느 클래스에 속하는지 매핑하기 위해 One-hot encoding을 적용하고 활성함수와 손실함수만 수정하면 된다. One-hot encoding에 대한 설명은 다음 포스트를 참고하면 된다.
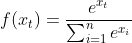

활성함수는 이진 분류에서 시그모이드 함수를 사용했다. 이때 0과 1사이의 값이 하나만 나왔다. 그러나, 우리는 여러 개의 클래스 n개를 분류하기 때문에 0과 1사이의 값이 n개가 필요하다. 그래서 다중 분류에서 사용하는 활성함수는 소프트맥스 함수(Softmax function)이다. (시그모이드 함수의 일반화)
우선 소프트맥스 함수의 항은 클래스의 갯수(n개)만큼 존재한다. 이는 각 클래스에 해당하는 확률값들을 의미한다. 각 항들은 "i번째 클래스일 확률 / 전체 확률"로 나타낸다.
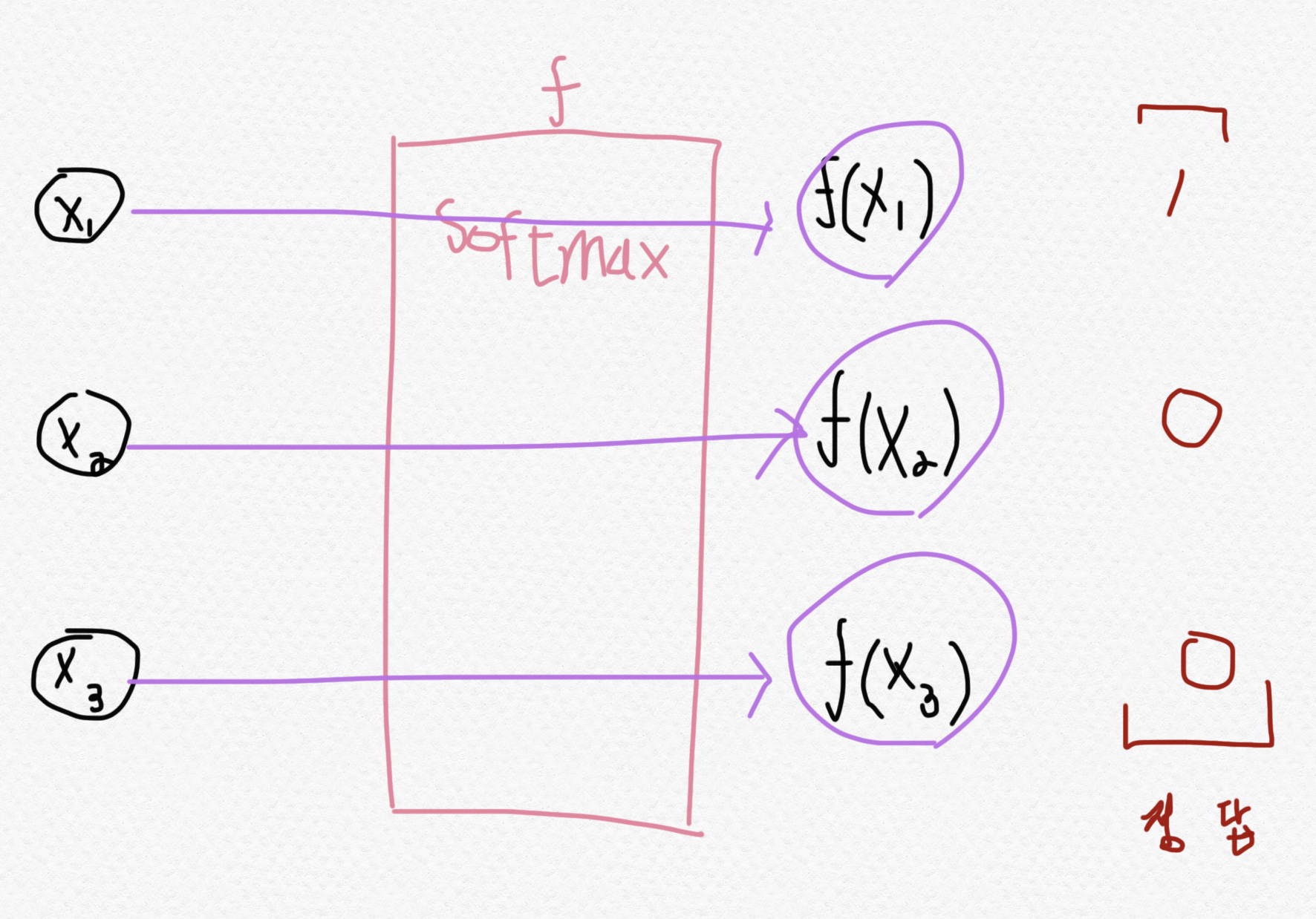
다음으로 크로스 엔트로피를 하기 이전에 해당 데이터에 대해 실제 정답을 One-hot encoding을 수행해야 한다.


이제 이진 분류가 아닌 다중 분류기 때문에 손실함수 또한 이진 크로스 엔트로피가 아닌 일반적인 크로스 엔트로피를 사용해야 한다. y'i 정답을 의미하고 (One-hot encoding : 해당하면 1, 해당하지 않으면 0), log(t)는 엔트로피를 의미한다. 즉, n개의 클래스중 정답에 해당하는 하나의 ∑ 항을 제외하고는 나머지는 전부 0이 된다. (두 번째 식의 예시에서는 2번째 클래스가 정답이기 때문에 One-hot encoding을 통해 나머지 클래스들의 정답은 0이 되므로 -log(t2) 항만 남는다.)
'[AI] - Machine Learning' 카테고리의 다른 글
| 군집화 알고리즘 (K-Means Clustering) (0) | 2021.12.09 |
|---|---|
| 군집화 알고리즘 (Clustering Algorithm) (0) | 2021.12.06 |
| 회귀 알고리즘 (Ridge, Lasso, ElasticNet) (0) | 2021.11.30 |
| 선형성, 비선형성 (Linear, Non-linear) (0) | 2021.11.29 |
| 선형 분류와 선형 회귀 (Linear Classification & Linear Regression) (0) | 2021.11.09 |