이번 포스트에서는 선형 회귀 이외의 다른 회귀 알고리즘에 대해 다뤄본다.
결론부터 이야기하면 다음과 같다.
- Lasso = Linear Regression + L1 Regularization
- Ridge = Linear Regression + L2 Regularization
- ElasticNet = Linear Regression + L1 Regularization + L2 Regularization

우리는 학습을 하다보면 점점 Loss가 떨어지는 것을 확인할 수 있다. 하지만, 거기서 안심하면 안된다. 오버피팅(과적합)은 머신러닝 분야에서 항상 존재하는 이슈이다. 오버피팅을 방지하기 위한 기법은 여러가지가 존재한다. Dropout, Batch normalization, RandomCrop 등.. 여러가지 존재한다. 이번에는 그중에서 정규화에 대해서 다뤄보고자 한다.
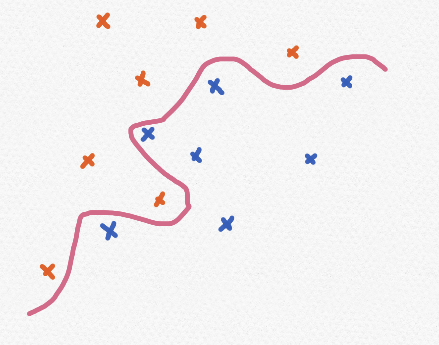
기하학적으로, 직관적으로 정규화를 표현하자면 오버피팅으로 인해 꾸불거리는 선을 펴는 것이다. 좀더 정확하게 말하면 데이터에 대하여 방정식을 일반화를 하는 것이다. 오버피팅이 발생하면 학습 데이터만 가지고는 분류하는 정확도가 매우 높을 것이다.
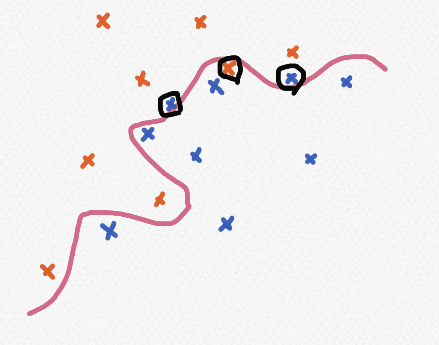
하지만, 새로운 데이터가 들어온 경우 오히려 정확도가 낮아질 수 있다. 그래서 우리는 학습 데이터의 정확도는 조금 떨어지더라도 그 외의 데이터는 구분할 수 있도록 일반화된 선이 필요하다.

지금부터 L1 정규화와 L2 정규화를 이해하기 위한 내용들을 천천히 살펴볼 것이다. 먼저 L1 Norm과 L2 Norm에 대해 알아보자. Norm은 벡터의 크기를 의미하며, 여기서는 두 벡터 사이에 차이를 여러가지 방식으로 표현하는데 그중 두 가지 방법을 살펴보는 것이다.
L1 Norm (Mahattan Distance)

L1 Norm은 두 벡터 사이의 각 요소의 차이의 절대값의 합을 의미한다. 예를 들어, 벡터 x = (3, 5, 9) 이고, 벡터 y = (-3, 4, -10) 일 때, |3-(-3)| + |5 - 4| + |9-(-10)| = 6 + 1 + 19 = 26이 된다.
L2 Norm (Euclidean Distance)

L2 Norm은 두 벡터 사이의 각 요소 차이의 제곱의 합에 루트를 씌운 것을 의미한다. 흔히 배운 거리 공식에 해당한다. 예를 들어, 벡터 x = (6, 3, 10) 이고, 벡터 y = (-1, -6, 9) 일 때, \sqrt{(6-(-1))^2 + (3-(-6))^2 + (10-9)^2} = \sqrt{49 + 81 + 1} = \sqrt{131} = 11.445523142.. 가 된다.

L1 Loss

L1 loss는 L2 loss에 비해 상대적으로 robust(이상치 및 에러값에 강건한) 성질을 지니고 있다. 하지만, y_{true}와 y_{predict}의 차이가 0인 지점에서는 미분이 불가능한 단점이 존재한다. (좌극한과 우극한이 다르기 때문이다. (참고))
L2 Loss

L1 loss에 비해 상대적으로 안정적이게 loss를 얻을 수 있다. (부드러운 곡선형태이므로 어디서나 미분가능) 하지만, 제곱이 존재하므로 이상치가 존재할 경우, loss 값이 지수적으로 높아지는 성질이 존재한다.
Regularization
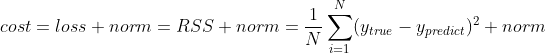
최종적으로 우리가 원하는 손실함수는 위와 같은 형태이다. 기존에 존재하던 loss(MSE 혹은 RSS : Residual Sum of Square)에 weight가 과도하게 커지는 것을 방지하기 위해 norm을 추가한다. 우리는 위와 같은 형태의 손실함수를 편미분을 통해 최소화 시키는 방향으로 파라미터들을 업데이트 해나가야 한다.
L1 Regularization


alpha 값은 하이퍼 파라미터이다. 그리고 L1 norm에 대해 미분을 진행하면 부호함수를 도출해낼 수 있다.
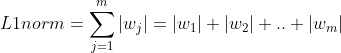

만약 norm을 w1에 대해 편미분을 진행했다고 가정하자. 나머지 w2 ~ wm은 상수취급 되어 사라지고, w1만이 남게 되는데 이마저도 절대값에 대한 미분이라서 스칼라(값의 크기)는 무시되고 w1의 부호에 따라 1, 0, -1의 결과만 나오게 된다. 그리고 가중치(w)가 0인 피처는 norm마저도 0으로 나와버리기 때문에 update를 진행하지 않음으로 제외된다. (feature extraction 효과)
L2 Regularization

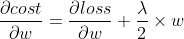
L2 Regularization은 L1 Regularization와 반대로 피처를 0으로 만들지는 않기 때문에 feature extraction 효과는 없다. 하지만, L1 Regularization은 극단적으로 업데이트 하는 반면에 L2 Regularization은 일반화를 smooth하게 진행한다.
ElasticNet Regrssion

ElasticNet Regression은 lambda1과 lambda2를 조절하여 L2 Norm과 L1 Norm을 조절할 수 있다.
'[AI] - Machine Learning' 카테고리의 다른 글
| 군집화 알고리즘 (Clustering Algorithm) (0) | 2021.12.06 |
|---|---|
| 선형 분류 (Linear Classification) (0) | 2021.12.03 |
| 선형성, 비선형성 (Linear, Non-linear) (0) | 2021.11.29 |
| 선형 분류와 선형 회귀 (Linear Classification & Linear Regression) (0) | 2021.11.09 |
| GBM (Gradient Boosting Machine) (0) | 2021.11.06 |