이번 포스트에서는 선형 분류와 선형 회귀에 대해 다뤄본다. 본 내용을 이전에 지도 학습(Supervised Learning)에 대해 간단하게 다루고 넘어가겠다. 지도 학습은 입력 데이터와 정답 데이터가 같이 주어져 학습하는 방식을 의미한다. 즉, 학습할 때 입력 데이터를 통해 머신러닝 모델이 예측한 데이터와 정답 데이터를 비교하면서 생기는 오차(Residual)를 보정해나가는 것을 의미한다.
근데 왜 갑자기 지도 학습에 대해 언급을 했을까? 그것은 지도 학습의 대표적으로 분류(Classification) 문제와 회귀(Regression) 문제가 있기 때문이다.
분류와 회귀는 둘다 예측 알고리즘이다. 그러나 무엇을 예측하는지가 다르다. 분류는 이산적인 값을 예측하는데에, 회귀는 연속적인 값을 예측하는데에 사용된다. 그림을 통해 알아보자.
(여기서 이산적인 값은 0, 1 이나 종류 혹은 클래스처럼 연속적이지 않은 값을 의미한다.)

위 그림은 직접 그린 발그림이다. 왼쪽은 분류에 대한 내용을, 오른쪽은 회귀에 대한 내용을 그린것이다. 분류와 회귀 모두 예측 알고리즘이라 했다. 무엇을 예측하느냐? 선의 기울기와 절편을 예측하는 것이다. 즉, 선의 위치를 예측하는 것이 목적이다. (결국에는 머신러닝은 기하학적 문제로 해석할 수 있다.)
먼저 분류에 대해 다뤄보면, 보라색 데이터와 빨간색 데이터가 선으로 인해 나눠진 것이 보일 것이다. 물론 완벽하게 두 종류의 데이터를 분리해낼 수 없다. 하지만, 두 종류의 데이터의 경계(Decision boundary)를 가장 일반적으로 표현할 수 있는 선을 찾는 것이 목표이다. 분류에 대한 오차는 시그모이드 (Sigmoid : 이진분류), 소프트맥스 (Softmax : 다중분류), 크로스 엔트로피 (Cross-entropy)로 정의하며 크로스 엔트로피를 최소화 시키는 선의 기울기와 절편을 찾는다.
회귀는 파란색들의 데이터에 가장 근접한 선을 찾는 것이 목표이다. 직관적으로 우리가 저 파란색 데이터를 직선 하나로 표현해야 한다면 오른쪽처럼 그리지 않을까? 수학적으로는 최소제곱법(Least Squared Method)이 사용된다. 최소제곱법이 무엇인지 간략하게 살펴보자.
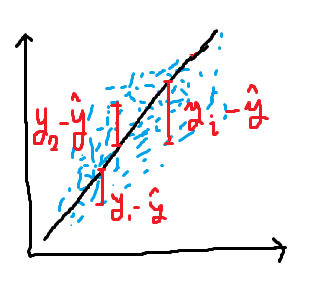


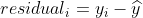
N개의 파란색 데이터(Pi)가 존재한다고 가정하자. 그리고 우리가 예측한 선은 y_hat 일 때, 오차(residual)는 실제 데이터(yi) - 예측 데이터(y_hat)이다.
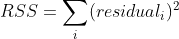
그렇다면 최종적으로 회귀는 이 오차를 최소화 하는 선을 찾는 것이 목표이다. N개의 데이터에 대해 모든 잔차를 더할때 우리는 데이터가 선보다 위에 있는 경우에는 이 오차가 음수가 될 수 있음을 안다. 그럴 경우 양의 수를 갖는 오차는 상쇄되어 정확한 정보를 얻을 수 없다. 고로, 오차의 제곱을 하여 부호를 없앤 후에 전부 합한다. (거리의 개념으로 변형)

그리고 합한 결과를 최소화 시킬 수 있는 파라미터 a와 b (앞서 언급한 우리가 예측해야할 선의 기울기와 절편) 를 찾는 것이 최소제곱법이다.
본론으로 돌아와, 우리는 결론적으로 RSS (Residual Sum of Square : 잔차 제곱의 합)을 최소화 시키는 방향으로 회귀계수 (파라미터 a와 b : 기울기와 절편)을 찾아나가는 방향으로 업데이트를 해야한다. 우리가 그럼 '업데이트'라는 키워드를 논하는 순간 바로 떠올라야 할 개념이 하나 있다. 그것은 바로 경사하강법 (Gradient descent)이다. 경사하강법에 대한 내용은 이전 포스트를 참고하자.
+ 머신러닝에는 여러가지 손실함수가 존재하며 그중 하나가 RSS이다. (ex - MSE, RMSE, RMSLE, ..)
이제부터 수식이 더 많이 들어가면서 어려워질 수 있지만, 침착하게 따라가보자. 먼저 이전 포스트의 내용을 참고하면서 리마인드 해보자면, 우리는 에러를 낮추는 방향으로 파라미터를 업데이트하는 것이 경사하강법이라는 사실을 안다. 그렇다면, 에러를 낮추는 방향을 어떻게 알까? 그것은 바로 편미분이다.
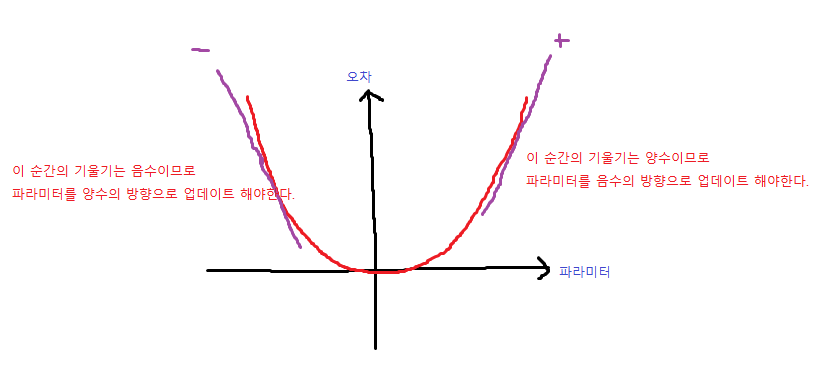
미분은 함수의 순간기울기를 알 수 있다. 그렇다면, 곡선 형태의 함수가 존재한다고 가정하자. 그 함수의 기울기가 양수일 경우, 파라미터를 양수의 방향으로 더하여 업데이트를 하면 점점 오차는 커질것이다. 고로, 우리는 미분값(기울기)의 음의 방향으로 파라미터를 업데이트 해야한다.
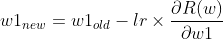
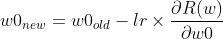
새로운 파라미터는 이전 파라미터에서 순간기울기의 반대방향으로 학습률 (lr : learning rate)만큼 업데이트 해야한다.


이제 순간기울기에 대해서 알아볼 차례이다. 위 공식에서 R은 잔차에 의한 오차함수를 의미한다. 그리고 w1과 w0에 대해 각각 편미분을 진행한다. w1과 w0는 위에서 언급한 파라미터 a와 b가 되겠다. (기울기와 절편)
'[AI] - Machine Learning' 카테고리의 다른 글
| 회귀 알고리즘 (Ridge, Lasso, ElasticNet) (0) | 2021.11.30 |
|---|---|
| 선형성, 비선형성 (Linear, Non-linear) (0) | 2021.11.29 |
| GBM (Gradient Boosting Machine) (0) | 2021.11.06 |
| 앙상블 기법 (Ensemble) (0) | 2021.10.28 |
| 의사 결정 나무 (Decision Tree) (0) | 2021.10.24 |