P.S. 대생성의 시대에서 Diffusion이나 GPT류들이 판치고 있는 시대에.. 이제서야 이 논문을 다루게 되네요.. ㅋ.ㅋ.ㅋ 많이 늦은 감이 없지않아 있지만, 복습할 겸 2018년 구글에서 발표한 Transformer에 대해 최대한 쉽게 정리해보려 합니다. 그래도 기본적인 RNN과 CNN에 대해서 공부하시고 오셔야 아래 내용을 이해할 수 있습니다!
Abstract
기존의 모델은 encoder와 decoder 구조로 되어 있으며, 해당 구조들은 RNN 혹은 CNN으로 구성되어 있다. 그리고, Attention 매커니즘을 적용하여 이들의 성능을 좀더 끌어올렸다. 본 논문에는 RNN과 CNN을 배제한 온전히 Attention 매커니즘으로만 구성되어 있는 새로운 아키텍처 Transformer를 제안하고자 한다. 기계 번역 태스크를 기준으로 Transformer는 학습에 더 적은 시간이 소요됨에도 불구하고, 우월할 성능을 보여주었다. (병렬 연산을 극대화한 케이스이다.)
1. Introduction
- RNN, LSTM, GRU와 같은 순환 신경망은 language modeling과 machine translation과 같은 태스크들에 대해 SOTA 성능을 달성해왔다.
- 순환 신경망은 일반적으로 입력과 출력 시퀀스의 위치에 따라 연산을 순서대로 수행한다. 연산 순서를 정하기 위해 입력 토큰들의 위치를 정렬하고, $t$번째 입력과 이전 은닉 상태 $h_{t-1}$를 반영하여 새로운 현재의 은닉 상태 $h_{t}$를 생성한다.
- 하지만, 이러한 방식의 연산은 새로운 은닉 상태를 생성하기 위해서는 이전 은닉 상태가 먼저 연산이 되어야 하기 때문에, 병렬화가 배제될 수 밖에 없다. 결국 순환 신경망은 시퀀스의 길이가 길어지면 연산 속도나 메모리 등 문제가 발생할 수 밖에 없다.
- 이러한 문제를 해결하기 위해, factorization trick이나 conditional computation과 같은 (e.g. 행렬 분해) 연산의 효율성을 증대시켰지만, 근본적으로 시퀀스의 길이가 길어질때 나타나는 문제는 해결하지 못했다.
- 이 후, Attention 매커니즘을 순환 신경망에 적용했지만, 근본적인 문제는 해결할 수 없을 뿐더러 단순 conjuction에 불과했다.
- 본 논문에서는 이들을 전부 배제하고, Attention 매커니즘만을 통해 아키텍처를 구성한 Transformer를 제안한다. Transformer의 contribution은 다음과 같다.
- 입력과 출력 사이에 global dependency를 극복
- 병렬 연산 극대화
2. Background
(생략)
3. Model Architecture
- 최근 sequence model에서 가장 좋은 성능을 보이고 있는 것은 seq2seq (encoder-decoder) 아키텍처이다.
- encoder는 입력 시퀀스 $x = (x_1, ..., x_n)$를 continuous representation $z = (z_1, ..., z_n)$으로 매핑한다.
- decoder는 encoder에서 생성된 $z$를 통해 출력 시퀀스 $y = (y_1, ..., y_m)$을 생성한다.
- 각 타임스텝별로 encoder와 decoder는 autoregressively하게 동작한다.
- 예를 들면, 타임스텝 $t=1$ 시점에서, encoder에 $x_1$이 입력으로 주어지면 encoder의 초기 은닉 상태 $h_1$와 함께 연산되어 $x_2$가 생성되고, encoder의 은닉상태는 $h_2$로 갱신된다.
- 그 다음 타임스텝 $t=2$에서는 생성된 $x_2$와 갱신된 은닉 상태 $h_2$가 함께 연산되어 $x_3$를 생성한다. 이러한 방식을 auto-regressive이라고 한다.
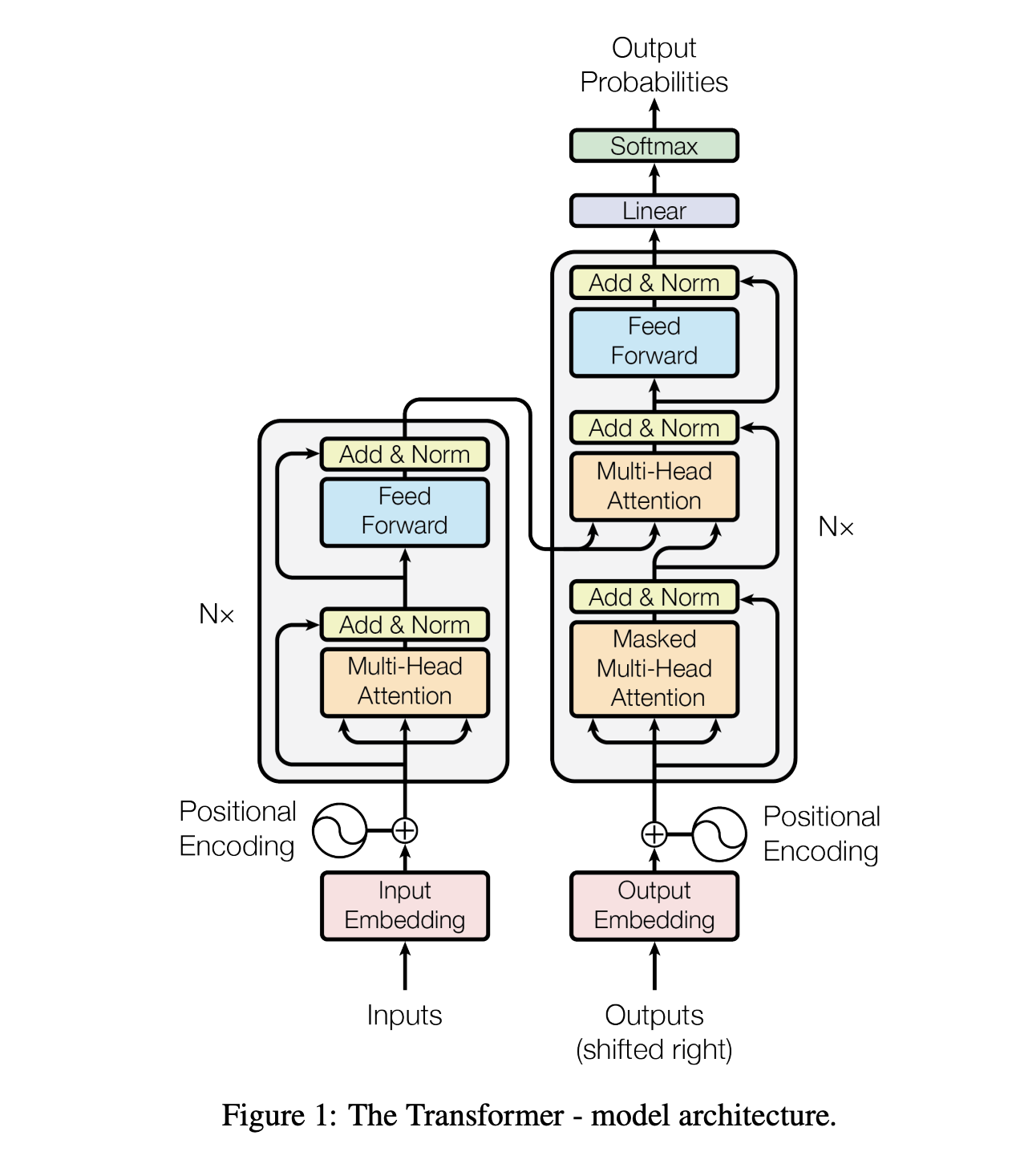
- 복잡해보이지만, Transformer는 다음과 같은 구조를 encoder와 decoder에 반복적으로 쌓아올린 것에 불과하다.
- self-attention
- point-wise
- fully-connected layer
- 좌측은 encoder, 우측은 decoder로 지금부터 encoder와 decoder를 차근차근 하나씩 뜯어볼 것이다. 설명을 그림과 대조해보며 읽는 것을 추천한다.
3.1. Encoder and Decoder Stacks
- Encoder
- encoder는 $N=6$개의 encoder layer로 구성되어 있다.
- 각 encoder layer에는 2개의 sub layer로 구성되어 있다.
- Multi-Head Self-Attention
- (Position-Wise Fully Connected) Feed-Forward
- 두 sub layer는 각각 residual connection이 포함되어 있으며, layer normalization이 뒤따른다.
- batch normalization같은 경우, 입력 데이터의 미니 배치들의 편향을 제거하기 위해 입력 feature들을 정규화하는 과정이다. (convariate shift 문제 해결 - 데이터의 분포가 레이어를 거듭할 수록 한쪽으로 편중되는 현상)
- layer normalization에 대해 간략히 설명하자면, 데이터의 크기가 절대적으로 커지면 미니 배치 또한 커질 수 밖에 없기 때문에 각 layer별 feature들을 정규화하는 것이다.
- 결국 이 과정들을 하나의 수식으로 정의하면 $LayerNorm(x + Sublayer(x))$가 된다.
- encoder를 통해 생성된 출력 시퀀스의 임베딩 벡터 차원은 $d_{model} = 512$차원이다.
- Decoder
- decoder 또한 $N=6$개의 decoder layer로 구성되어 있다.
- 각 decoder layer에는 encoder layer와 유사해보이지만, 1개의 sub layer가 추가되었다.
- Masked Multi-Head Attention
- Multi-Head Self-Attention
- (Position-Wise Fully Connected) Feed-Forward
- 유의해야할 점은, encoder의 출력 시퀀스 임베딩 벡터는 decoder의 중간 sub layer인 Multi-Head Attention의 입력에 포함되는 것이다.
- encoder와 동일하게 residual connection이나 layer normalization이 포함되어 있다.
- 새로 추가된 Masked Multi-Head Attention은 현재 연산해야 하는 토큰의 뒤에 오는 토큰들을 참조하지 않기 위해 사용된다.
- $i$번째 위치의 값을 생성할 때, $i$번째 이전만 참조하기 위함이다. 왜냐하면, decoder는 실질적으로 다른 도메인의 데이터를 생성해야 하는 영역으로써, autoregressive하게 동작해야 하기 때문이다.

3.2. Attention

- Attention 매커니즘은 query를 key-value의 집합을 통해 매핑하는 것으로 정의할 수 있다. 여기서 query, key, value는 모두 가중치 행렬 혹은 벡터를 의미한다. (학습 대상)
- 최종 출력은 value들의 weighted sum으로 이루어 지며, 여기서 각 value에 해당하는 weight는 query를 통해 요청한 key에 해당한다.
3.2.1 Scaled Dot-Product Attention
- Transformer 아키텍처에 적용된 기본적인 Attention 매커니즘인 Scaled Dot-Product Attention은 다음과 같은 입력들을 포함하고 있다.
- $d_k$ 차원의 query
- $d_k$ 차원의 key
- $d_v$ 차원의 value

- 하지만, 우리는 병렬 연산을 극대화할 것이기 때문에, 하나의 query가 아닌 다수의 query를 처리해야 하므로, 행렬 연산으로 Attention 매커니즘을 정의하면 다음과 같다.
- $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$
- query와 key를 dot product를 수행하여 가장 유사도가 높은 key vector를 찾아낸다. (dim=-1)
- 여기서 값이 너무 커지는 것을 방지하기 위해 $\sqrt{d_k}$를 통해 스케일링을 수행한다.
- 최종적으로, 스케일링을 수행한 key vector와 value vector를 곱한다.
- 여기서 유의해야 할 것은 query, key, vector는 모두 독립적인 학습 대상인 가중치 행렬이다.
3.2.2 Multi-Head Attention
- $d_{model}$ 차원의 key, value, query 행렬들을 하나의 Attention 함수로 수행하는 것보다는, $h$번 각기 다른 $d_k$, $d_k$, $d_v$차원으로 linear projection하는 것이 이점이라는 사실을 밝혀냈다.
- projection된 각각의 query, key, value들은 Attention 함수를 수행하는데, 이 과정이 총 $h$번 발생하는 것이다. 그리고, 각각의 Attention 함수의 출력 차원은 $d_v$가 될 것이다.
- 최종적으로, $h$개의 Attention 함수의 결과물들을 concatenate하여 결과를 산출한다.
- $MultiHead(Q, K, V) = Concat(head_1, ..., head_h)W^O$
- $where\ head_i = Attention(QW^Q_i, KW^K_i, VW^V_i)$
- $W^Q_i \in \mathbb{R}^{d_{model} \times d_k}$
- $W^K_i \in \mathbb{R}^{d_{model} \times d_k}$
- $W^V_i \in \mathbb{R}^{d_{model} \times d_v}$
- 본 논문에서는 Attention 함수를 병렬로 수행할 헤드 갯수를 $h = 8$로 설정했다.
- 최종적으로, 각 헤드에서 발생한 Attention 함수의 결과들을 concatenate할 것이기 때문에, $d_k = d_v = d_{model}/h = 64$로 설정했다.
- 쉽게 말해, 각 헤드에서 발생한 Attention 함수의 결과 벡터는 $d_{model}/h$ 차원으로 설정하여 이들을 모두 concatenate하는 것이다.
3.3 Position-wise Feed-Forward Networks
- encoder와 decoder의 Attention sub layer 이후에는 fully connected feed-forward network가 뒤따른다.
- fully connected feed-forward network는 두 번의 linear transformation이 이루어지고, 그 사이에 ReLU 활성화 함수를 한번 거친다.
- $FFN(x) = max(0, xW_1 + b_1)W_2 + b_2$
- max(0, xW_1 + b_1)이 ReLU 활성화 함수에 해당한다.
- 두 번의 linear transformation은 서로 다른 파라미터를 지니고 있다.
- linear transformation은 MLP로 이해할 수 있다.
- 입력과 출력 차원은 $d_{model} = 512$으로 동일하다.
- 두 MLP 레이어 사이의 차원은 $d_{ff} = 2048$ 차원이다.
3.4 Embeddings and Softmax
- 입력 토큰과 출력 토큰을 $d_{model}$차원의 벡터로 변환하기 위한 학습된 임베딩 테이블을 사용한다.
- 그리고, 학습된 linear transformation과 softmax 함수를 통해 decoder의 출력 임베딩을 다음 토큰의 확률로 표현한다.
- 또한, 두 개의 임베딩 레이어(input embedding, output embedding)는 서로 같은 가중치 행렬을 공유한다.
3.5 Positional Encoding
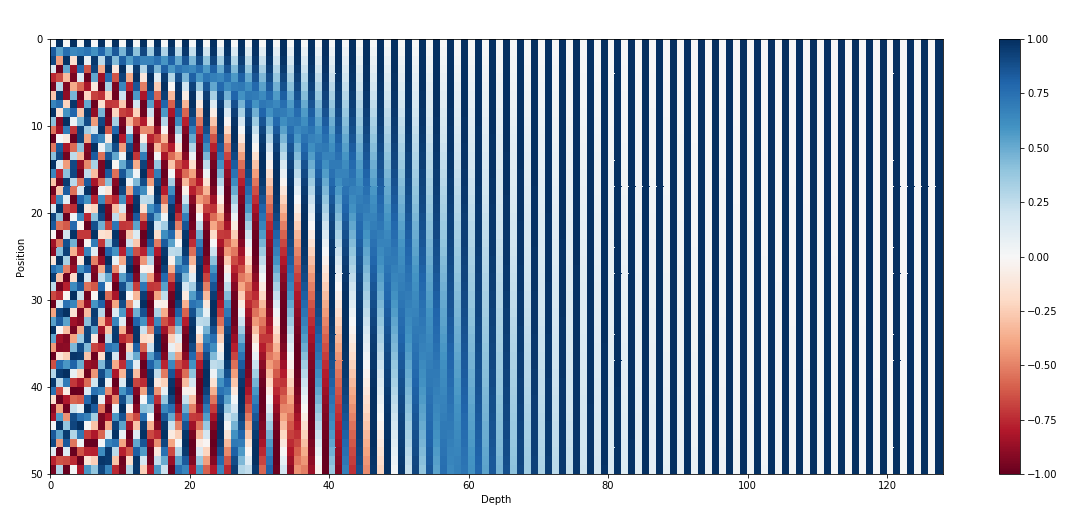
- Transformer 아키텍처의 경우, 순환 신경망 혹은 합성곱 신경망으로 구성되어 있지 않기 때문에 입력 시퀀스의 토큰들에 대한 순서 정보를 주입해주어야 한다. (Transformer 입장에서는 입력된 시퀀스 벡터에 대한 순서 개념이 없이 병렬로 처리하기 때문이다.)
- 위치 정보를 주입하기 위해 본 논문에서는 positional encoding라는 개념을 도입한다.
- 이는 encoder와 decoder의 시작부에 도입된다.
- positional encoding은 임베딩과 동일한 차원인 $d_{model}$차원이며, 임베딩 벡터와 더해져서 encoder 혹은 decoder의 입력으로 주어지게 된다.
- 아래는 positional encoding을 하기 위한 수식이다.
- $PE_{pos, 2i} = sin(pos/10000^{2i/d_{model}})$
- $PE_{pos, 2i+1} = cos(pos/10000^{2i/d_{model}})$
- $pos$는 위치를 의미하고 $i$는 임베딩 벡터의 차원을 의미한다.
- 즉, positional encoding 각 차원은 정현파(sinusoid)에 해당한다.
REFERENCE
'[독파하기] 논문' 카테고리의 다른 글
| # 3. Deep Residual Learning for Image Recognition (0) | 2022.05.15 |
|---|---|
| # 2. Going deeper with convolutions (0) | 2022.04.03 |
| # 1. Network In Network (0) | 2022.03.28 |
| # 0. ImageNet Classification with Deep ConvolutionalNeural Networks (0) | 2022.03.17 |




댓글