Abstract

신경망의 깊이가 깊어질수록 학습에 어려움이 존재한다. 해당 논문에서는 residual learning framework (잔차 학습 프레임워크)를 통해 신경망이 깊어지더라도 학습을 쉽게 할 수 있음을 제안한다. 해당 방법은 기존의 unreferenced functions 대신 인풋 레이어를 참조하는 (referenced) residual function을 학습하도록 명시적으로 수식을 다시 정의한다. (이 부분에 대해서는 뒷 부분에서 그림을 통해 다시 쉽게 설명할 것이다.)
이 학습방법의 효과로 VGG-19 네트워크를 8배 더욱 깊게 레이어를 쌓았음에도 불구하고 계산 복잡도가 더 낮았다. residual 네트워크들의 집합(앙상블)은 결국에는 ImageNet 데이터 셋에 대해 3.57%의 에러율은 보여주었다.
Introduction
심층 컨볼루션 신경망은 이미지 분류 문제에서 돌파구 역할을 했다. 깊은 신경망은 저수준부터 고수준의 피처들과 분류기들을을 조합하여, 각 수준(level)의 피처들은 겹겹히 쌓여있는 레이어들에 의해 강화될 수 있었다.
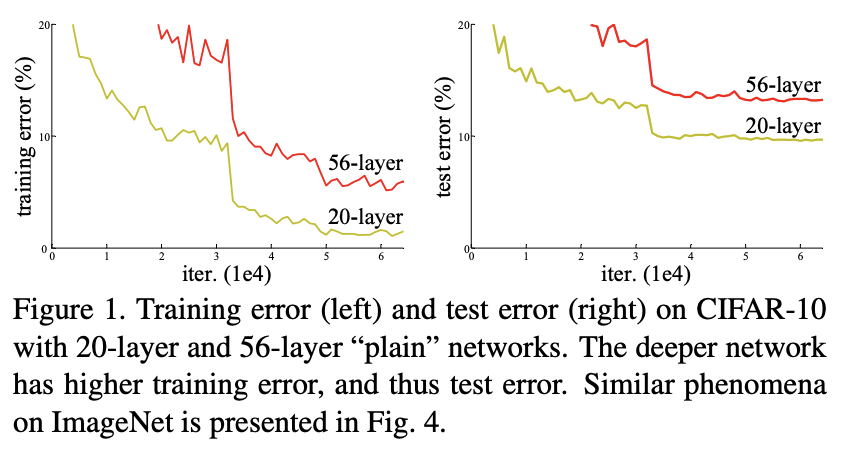
레이어가 깊어질수록 그레디언트 소실 및 폭주(gradient vanishing, exploding)과 같은 문제로 학습이 쉽게 되지 않았다. 이러한 문제는 초기화 기법(initialization)과 정규화 기법(normalization layers)를 통해 해결되었다. 하지만, 그럼에도 불구하고 신경망이 수렴할 수 있을 때 degradation 문제가 발생했다. degradation 문제는 신경망의 깊이가 증가함에 따라 정확도가 수렴하고 빠르게 급감하는 것을 의미한다. 그리고 이러한 문제는 오버피팅에 의해 발생하는 문제가 아니다.
degradation 문제는 최적화가 쉽지 않다는 것을 의미한다. 만약, 얕은 신경망과 깊은 신경망을 비교했을 때, 깊은 신경망이 얕은 신경망보다 에러율이 더 높지 않는다는 기대를 할 것이다. 그래서 degradation 문제를 해결하기 위해 고안한 방법은 identity mapping으로 레이어를 추가하고, 학습된 얕은 신경망으로부터 다른 레이어들을 복사해오는 것이다. 하지만, 이번 실험에서 현재 solver들이 찾은 솔루션 중에서 이러한 방법보다 비교적 좋은 방법을 찾지 못했다.
 |
 |
본 논문에서 degradation 문제를 해결하기 위해 deep residual learning framework를 소개한다. 각각의 조금씩 쌓여진 레이어들이 직접 underlying mapping을 학습하는 것보다, residual mapping을 학습하게 한다. underlying mapping은 기본 mapping인 $H(x)$라고 하자. 우리가 해야할 것은 그림처럼 쌓여진 비선형 레이어들이 underlying mapping이 아닌 다른 mapping인 $F(x) = H(x) - x$를 학습하게 하는 것이다. 그래서 original mapping을 $F(x) + x$로 바꿀 수 있다.
 |
 |
쉽게 설명하면, 왼쪽의 그림이 underlying mapping (original mapping), 오른쪽 그림이 residual mapping이다. 만약 original mapping의 경우 shortcut connection이 없으므로 비선형 함수의 모음인 $d(c(b(a(x))))$를 한번에 학습해야 한다. 하지만, residual mapping의 경우 shortcut connection이 있으므로 $b(a(x))$와 $d(c(y))$를 따로 학습할 수 있다.
직관적으로 설명하자면, 우리가 복습을 할때에 모든 문제를 기억에 의존해서 공부하는 것보다는 메모해둔 것을 바탕으로 메모 안한 부분만 학습하는 것이라고 생각할 수 있다.
Deep Residual Learning
Residual Learning

$H(x)$가 underlying mapping (original mapping)이라고 가정하자. 다중 비선형 레이어를 complicated functions로 근사시킬 수 있다고 가정하면, input과 output의 차원이 동일할 때 residual functions(i.e. $H(x) - x$)로 근사시킬 수 있다고 가정하는 것과 동일하다.
그러므로 우리가 학습시키기 위한 함수 $F(x) = H(x) - x$라고 정의할 수 있고, 결국 original mapping 인 $F(x)$를 $F(x) + x$로 재정의할 수 있다.

이러한 가정은 shortcut connection이 identity mapping이 최적이라고 가정할 때, identity mapping에 접근하기 위해 다중 비선형 레이어의 가중치를 0으로 쉽게 유도할 수 있다. ($F(x)$를 0으로 만드는 것을 초점으로 학습하기 때문에 학습 난이도가 낮아진다.)

실제로 shortcut connection이 identity mapping이 최적이 아닌 상황에서도 문제에 대한 precondition을 줄 수 있다. 최적의 함수가 zero mapping(original mapping)보다 identity mapping에 가깝다면, 작은 변화인 $F(x)$를 학습하는 것이 새로운 함수인 $H(x)$를 학습하는 것보다 쉬울 것이다.
Identity Mapping by Shortcuts
$y = F(x, W_{i}) + x$
residual learning을 적용하기 위해서는 다음과 같은 building block 수식을 정의한다. (Figure 2) $x$와 $y$는 input, output 벡터를 의미한다. 함수 $F(x, W_{i})$는 학습될 residual mapping을 의미한다.
$y = F(x, W_{i}) + W_{s}x$
$F$와 $x$의 차원은 일치해야 하기 때문에 다음과 같이 수식을 재정의한다. 행렬 $W_{s}$는 벡터 $x$의 차원을 F와 동일하게 맞춰주기 위함이다.
그리고, Figure 2의 그림대로라면 함수 $F$는 두 개의 weight layers를 가지고 있지만, 만약 하나의 layer밖에 없으면 선형 연산이므로 큰 이점이 없다.
Network Architectures
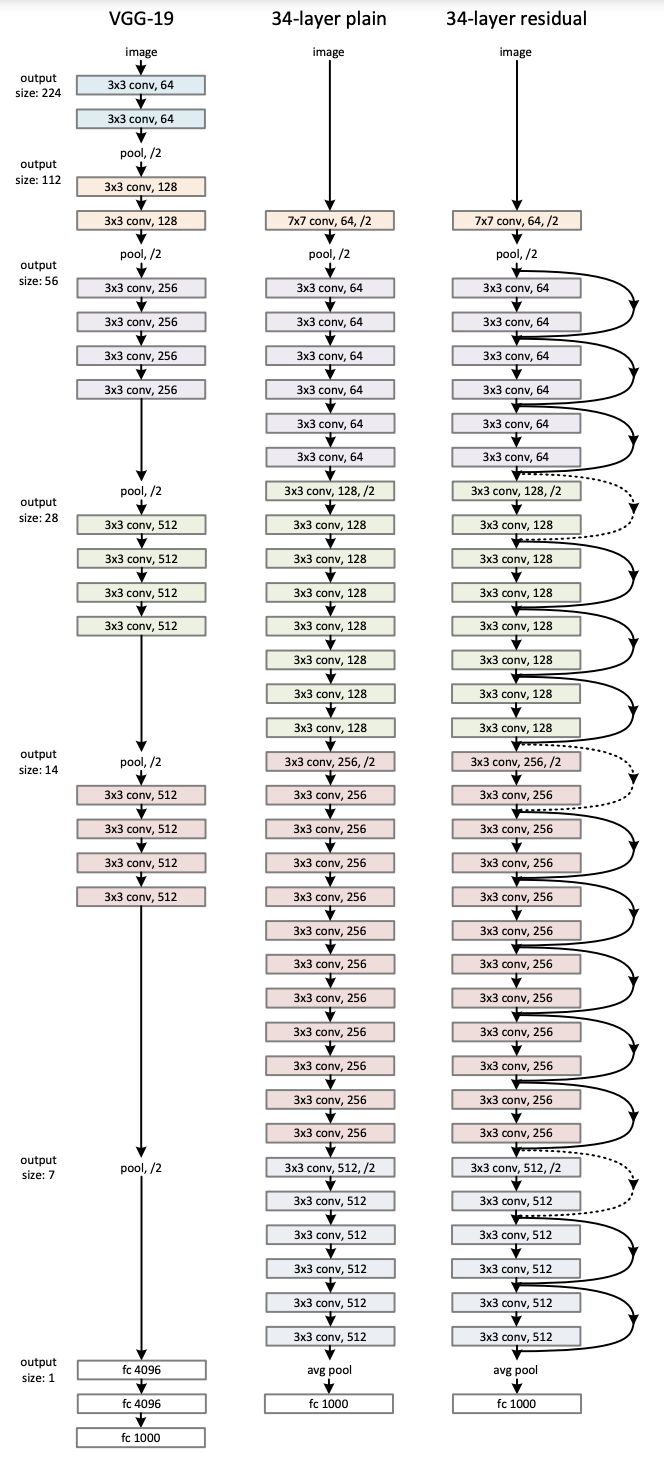
Experiments
ImageNet Classification
Plain Networks vs Residual Networks
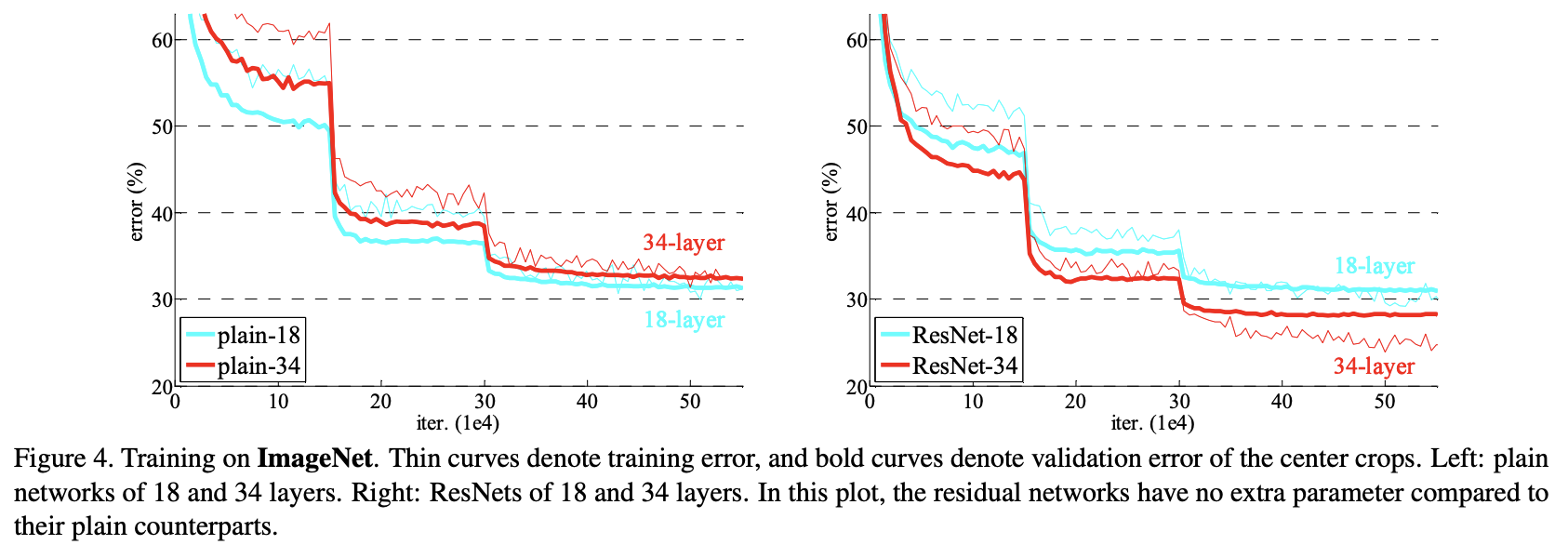
좌측은 residual mapping을 사용하지 않은 네트워크를 의미하고, 우측은 residual network를 의미한다. Top-1 에러율을 보면 알다시피, plain network 같은 경우는 레이어의 깊이가 깊어질수록 높아지는 것을 확인할 수 있다. 반면에, residual network는 그와 반대되는 결과를 도출한다.
plain network 같은 경우에는 BN (Batch Normalization)을 사용하기 때문에 순전파가 0이 아닌 분산을 갖는 신호가 흐르는 것을 확인할 수 있다. 고로, vanishing gradient의 문제로는 볼 수 없다.
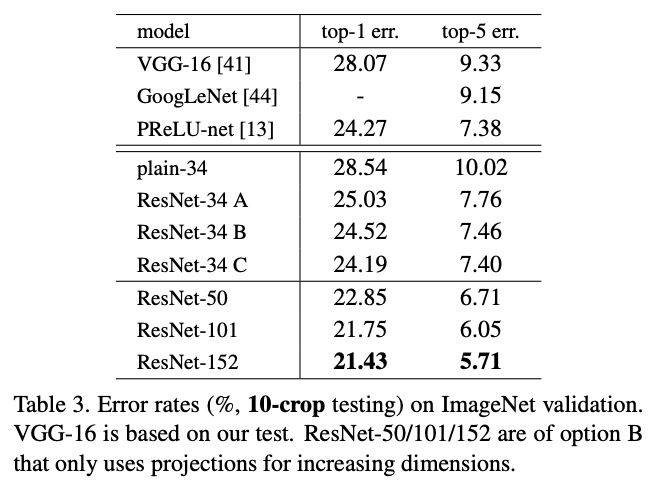
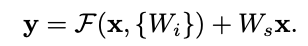
residual network 같은 경우에는 3가지 옵션으로 에러율이 측정되었다.
- option A : identity mapping + zero padding
(plain network에 비해 추가적으로 학습해야할 파라미터를 늘리지 않도록 identity mapping과 차원을 동일하게 맞춰주기 위한 zero padding으로 이뤄져 있는 채널을 사용)
- option B : identity mapping + projection shortcut
- option C : only projection shortcut
C 옵션의 성능이 가장 좋았지만, 해당 논문에서는 모델의 복잡도(complexity)와 크기(size)의 증가를 없애기 위해 사용하지 않았다. identity shorcut이 뒤에서 설명할 bottlenetck 아키텍처에서 복잡도를 증가시키지 않기 위해 중요한 요소이다.
Deeper Bottleneck Architectures
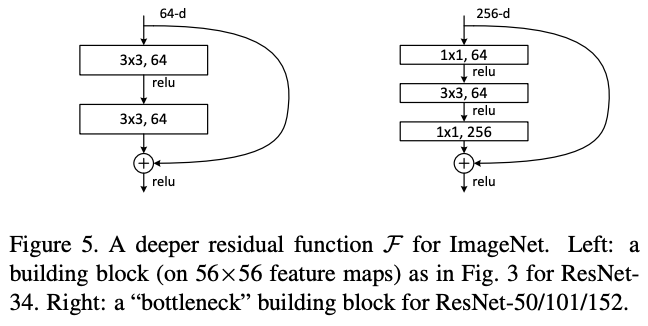
위 그림에서 좌측이 처음에 소개한 building block architecture이고, 우측이 bottleneck architecture이다. 우측처럼 설계한 이유는 학습시간을 고려한 까닭이다. Network In Network 논문 리뷰에서도 언급했다시피 $1 \times 1$ convolution 연산은 차원을 조절하기 위한 목적으로 존재한다. (첫 번째 $1 \times 1$ conv는 차원을 줄이고 두 번째 $1 \times 1$ conv는 차원을 늘려 원래대로 복원)
'[독파하기] 논문' 카테고리의 다른 글
| # 4. Attention Is All You Need (0) | 2023.06.07 |
|---|---|
| # 2. Going deeper with convolutions (0) | 2022.04.03 |
| # 1. Network In Network (0) | 2022.03.28 |
| # 0. ImageNet Classification with Deep ConvolutionalNeural Networks (0) | 2022.03.17 |




댓글