# 6. np.meshgrid

이번 포스트에서는 격자형 그리드를 생성하는 방법에 대해 포스팅한다. 격자형 그리드란 공간에서 일정한 간격으로 포인트를 찍은 것을 말한다. 격자형 그리드를 통해 특정 데이터 공간을 명확하게 그릴 수 있다. 이를 테면 아래와 같이 그릴 수 있다.

 

 

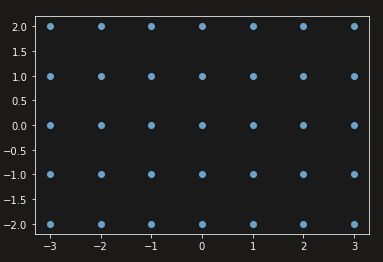
x = np.linspace(-3, 3, 7) # array([-3., -2., -1.,  0.,  1.,  2.,  3.])
y = np.linspace(-2, 2, 5) # array([-2., -1.,  0.,  1.,  2.])

x, y = np.meshgrid(x, y)
print(x.shape, y.shape)
>>>
(5, 7) (5, 7)

x와 y를 일정한 간격으로 포인트를 찍는 함수인 np.linspace를 호출하여 구성했다. 주어진 x, y에 대하여 np.meshgrid를 호출하면 새로운 2차원 공간에 대한 x, y가 생성되었다. 그럼 이제 x와 y에 대해서 살펴보자.

(np.meshgrid() 함수의 indexing='xy'가 디폴트, 'ij'를 옵션으로 줄 수 있다.)

 

indexing='xy' vs 'ij'

파라미터의 옵션에 따라 행렬의 위치를 표기하는 방법이 달라진다. 왼쪽(indexing='xy')은 직교좌표계를 따르고, 오른쪽(indexing='ij')는 행렬에서의 인덱싱을 따른다. 고로, 두 행렬은 서로 전치(Transpose)관계에 놓여있다.

 

# indexing='xy'

x
>>>
array([[-3., -2., -1.,  0.,  1.,  2.,  3.],
       [-3., -2., -1.,  0.,  1.,  2.,  3.],
       [-3., -2., -1.,  0.,  1.,  2.,  3.],
       [-3., -2., -1.,  0.,  1.,  2.,  3.],
       [-3., -2., -1.,  0.,  1.,  2.,  3.]])
       
y
>>>
array([[-2., -2., -2., -2., -2., -2., -2.],
       [-1., -1., -1., -1., -1., -1., -1.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 1.,  1.,  1.,  1.,  1.,  1.,  1.],
       [ 2.,  2.,  2.,  2.,  2.,  2.,  2.]])

# indexing='ij'

x
>>>
array([[-3., -3., -3., -3., -3.],
       [-2., -2., -2., -2., -2.],
       [-1., -1., -1., -1., -1.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 1.,  1.,  1.,  1.,  1.],
       [ 2.,  2.,  2.,  2.,  2.],
       [ 3.,  3.,  3.,  3.,  3.]])

y
>>>
array([[-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.]])

plt.scatater(x, y)

두 옵션의 결과는 동일하다.

 

sparse=True

x, y = np.meshgrid(x, y, sparse=True)
print(x.shape, y.shape)
>>>
(1, 7) (5, 1)

x
>>>
array([[-3., -2., -1.,  0.,  1.,  2.,  3.]])

y
>>>
array([[-2.],
       [-1.],
       [ 0.],
       [ 1.],
       [ 2.]])

메모리를 절약하기 위해 반복적으로 stack이 되는 구조를 제거한 희소 그리드이다. 

 

참고

https://numpy.org/doc/stable/reference/generated/numpy.meshgrid.html

numpy.meshgrid — NumPy v1.22 Manual