# 0. 기초통계 - 확률, 우도, 조건부확률

P.S. 해당 블로그에서 다룰 통계 개념은 딥러닝을 쉽게 이해기 위한 개념들을 중심으로 정리하려고 합니다. 생성(Generative) 분야는 특정 확률 분포 공간에서 가장 그럴듯한 데이터를 샘플링하기 때문에 확률과 통계 개념이 중요합니다. 물론 꼭 생성 분야가 아니더라도 다양한 도메인에서 적용될 수 있습니다.

 

모수 (Parameter)

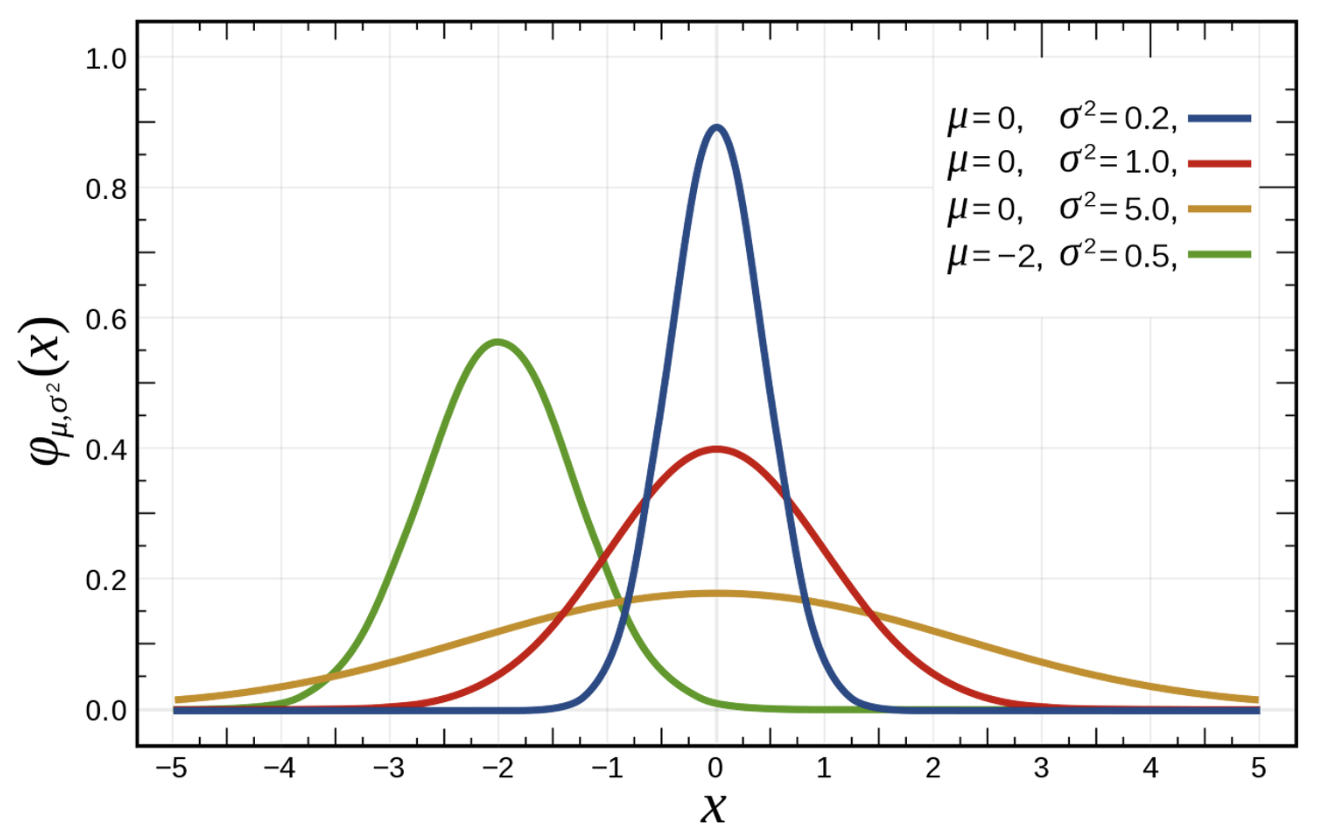
• 모수란 특정 확률 분포에 대한 특성값을 의미한다.
• 위와 같은 4개의 확률 분포는 동일한 정규 분포의 형태를 띄더라도, 서로 다른 모수(평균 $\mu$와 분산 $\sigma^2$)에 따라 다른 형태를 띄고 있음을 알 수 있다.
• 일반적으로 모집단을 전수조사할 수 없기 때문에 우리는 표본 추출(Sampling)을 통해 표본 집단에 대한 모수로 모집단의 모수를 추정한다.

 

확률 VS 우도

 

확률 (Probability)

• $P(A) = \frac{사건\ A에\ 해당하는\ 샘플의\ 수}{표본\ 공간에\ 존재하는\ 샘플의\ 수}$
• 확률은 특정 모수가 주어졌을 때, 특정 사건이 발생할 비율을 의미한다.
  • 특정 확률 분포에서 면적을 의미한다.
• 예를 들면, 암 진단용 시약 검사에서 양성이 나온 집단이 100명이고, 이중에서 실제로 암에 걸린 사람이 80명이라면, "시약 검사에서 양성이 나온 경우 암에 걸릴 확률은 80%"라고 할 수 있다.
  • 양성인 집단은 표본 공간의 샘플의 수에 해당하고,
  • 암에 걸린 사람의 수는 사건 A에 해당하는 샘플의 수에 해당한다.

 

우도 (Likelihood)

• $P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{P(A,B)}{P(A)}$
• 어떤 현상 A가 발생했을 때, 해당 현상 A가 집단 B에 나타날 확률을 의미한다.
  • 특정 확률 분포에서 높이(확률 분포의 값)을 의미한다.
• 예를 들면, 실제로 암이 걸린 사람을 대상으로 암 진단용 시약 검사를 했더니 99%가 양성으로 나온 경우, 우도는 99%라고 할 수 있다.
  • 실제로 암이 걸린 사람은 현상 A에 해당하고,
  • 양성으로 나온 집단은 집단 혹은 특정 확률 분포 A에 해당한다.
• 다음과 같이 변형이 가능하다.
  • $P(A \cap B) = P(A, B) = P(B|A)P(A) = Likelihood \times Prior\ Probability$

 

조건부확률 (Conditional Probability)

• $P(A|B) = \frac{P(A)P(B|A)}{P(B)}$
  • $Posterior\ Probability = \frac{Prior\ Probability \times Likelihood}{Evidence}$
• 조건부확률은 특정 표본집단 B이 발생할 확률 내에서 사건 A가 발생할 확률을 의미한다.
  • 예를 들어, 전체 인원은 200명이고 암 진단용 시약 검사에서 양성이 나온 표본집단은 100명인 경우 $P(B) = \frac{100}{200}$이다.
  • 암이 발생한 환자에 대한 확률은 $P(A)$다.
  • 하지만, 암이 발생한 환자가 무조건 양성이 나온 집단에만 있으라는 보장은 없다. 반대의 말로 표현하자면 음성 집단에서도 발생할 확률이 존재하는데, 우리가 원하는 것은 양성이 나온 집단 내에서 암인 환자에 대한 확률이기 때문에 우도 $P(B|A)$를 곱한 것이다.